Question

How do you solve `2cosx+3=0`?

Answer 1

`x = (2k+1)pi +- ln((3+sqrt(5))/2) i" "` for any integer `k`

Explanation:

Given:

`2 cos x + 3 = 0`

Subtracting `3` from both sides and dividing by `2` this becomes:

`cos x = -3/2`

This is outside the range `[-1, 1]` of `cos x` as a real valued function of real values. So there are no Real solutions.

What about complex solutions?

Euler's formula tells us:

`e^(ix) = cos x + i sin x`

Taking conjugate, we get :-

`e^(-ix) = cos x - i sin x`

Hence on adding above two equations we get :-

`cos x = 1/2(e^(ix) + e^(-ix))`

So the given equation becomes:

`e^(ix) + e^(-ix) + 3 = 0`

Multiplying by `4e^(ix)` and rearranging slightly:

`0 = 4(e^(ix))^2+12(e^(ix))+4`

`color(white)(0) = (2e^(ix))^2+2(2e^(ix))(3)+9-5`

`color(white)(0) = (2e^(ix)+3)^2-(sqrt(5))^2`

`color(white)(0) = (2e^(ix)+3-sqrt(5))(2e^(ix)+3+sqrt(5))`

So:

`e^(ix) = (-3+-sqrt(5))/2`

So:

`ix = ln((-3+-sqrt(5))/2) + 2kpii`

`color(white)(ix) = +-ln((3+sqrt(5))/2) + (2k+1)pii`

for any integer `k`

So:

`x = (2k+1)pi +- ln((3+sqrt(5))/2) i`

Answer 2

No solutions for `x in RR`

Explanation:

`2cosx+3=0`

Subtract `3` from both sides and divide by 2:

`cosx=-3/2`

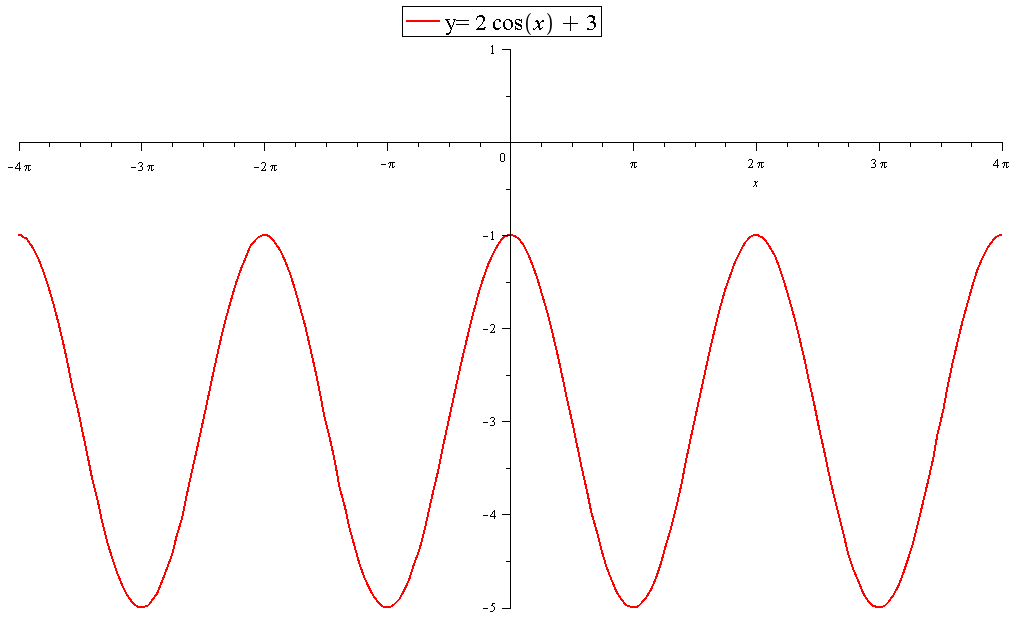
This show that the equation has no real solutions. We know this because:

`-1<=cosx<=1`

The graph of `y=2cos(x)+3` confirms this: