How do you solve #2x^2-12x=-14# by completing the square?
2 Answers
Explanation:
Write as
What process we are about to do introduces a value that is not in the original equation. So we mathematically compensate for this by the inclusion of a correction value. This correction value would turn the introduced error into 0 if we were to carry out the addition.
Suppose we had
Let
Write as
Move the power of 2 to outside the bracket
divide the 6 from
Discard the
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
The error comes from the
So the error is
This has to be turned into 0 by
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Write as:
Square root both sides
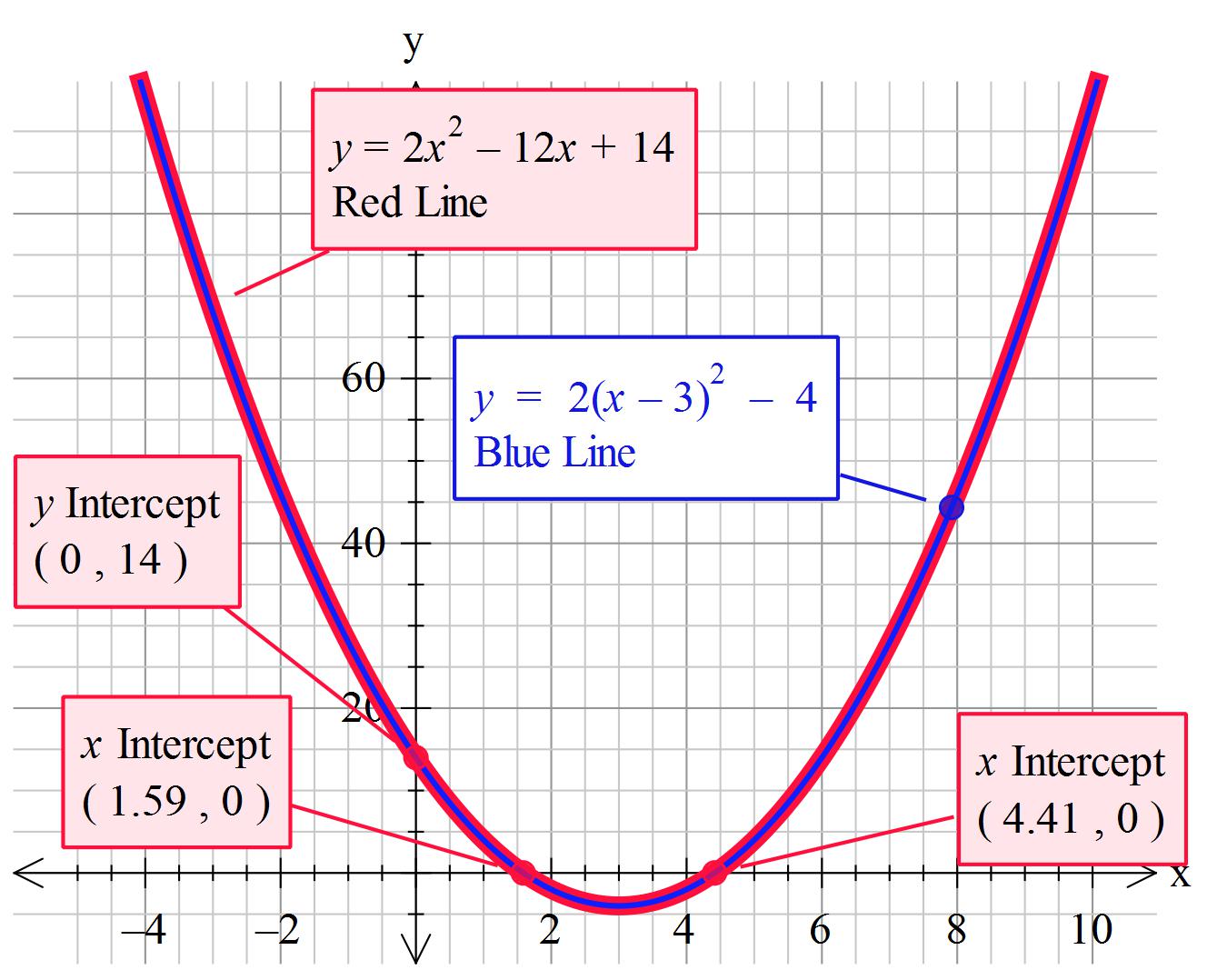
Explanation:
Completing the square is based on the consistency of the answers to the square of a binomial.
In all of the products above,
The first and last terms,
There is a specific relationship between 'b' - the coefficient of the
Knowing this, it is always possible to add in a missing value for
In
This gives:
NOW the correct value of
This gives 2 possible answers for


