Question

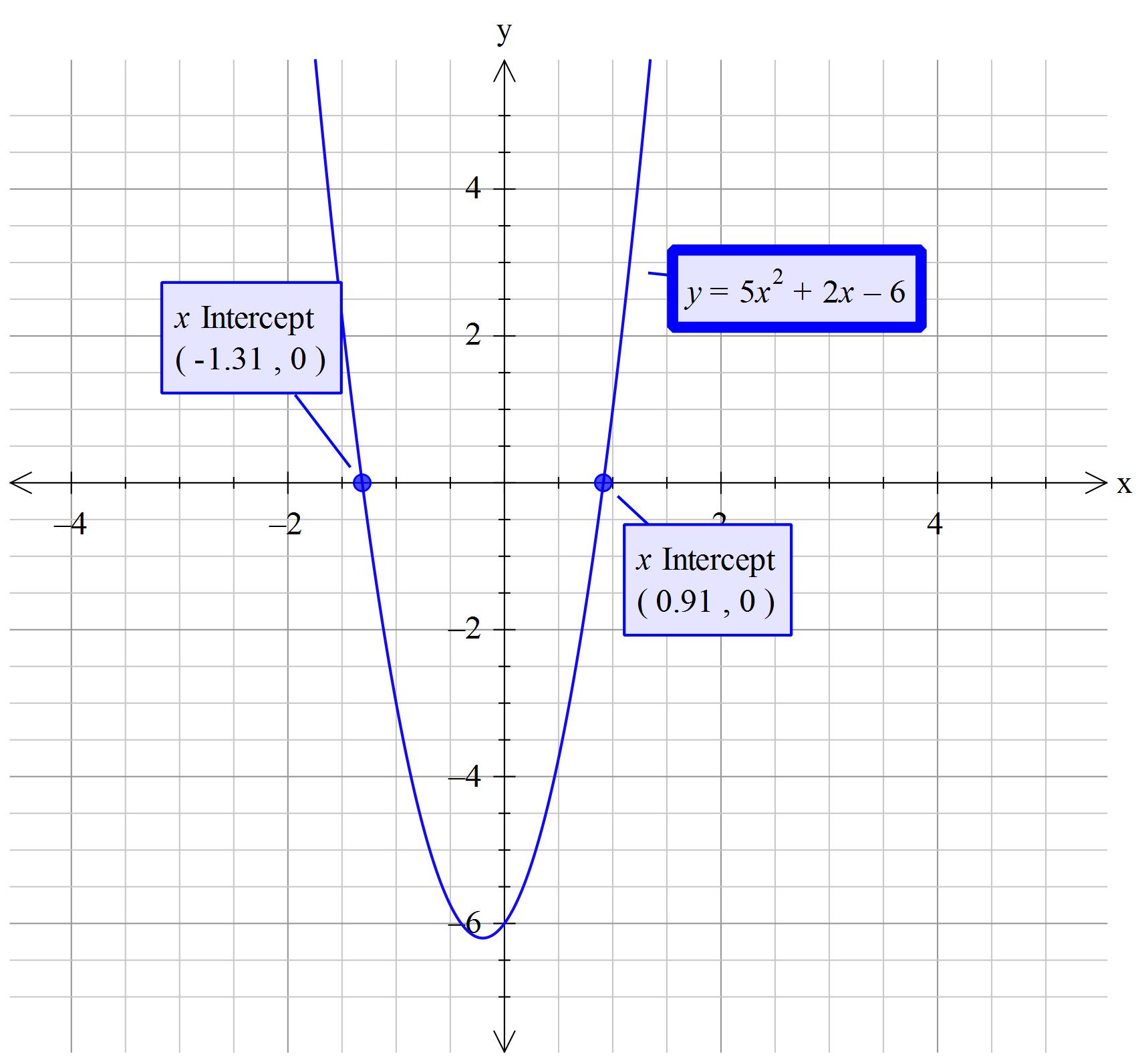
How do you solve `2x - 6 = -5x^2` by completing the square?

Answer 1

`x=-1.313` to 3 decimal places

`x=+0.914` to 3 decimal places

Explanation:

Standard form `-> y=ax^2+bx+c`

Converting the given equation to standard form gives

`y=0=5x^2+2x-6`

But `y=0` is a specific case

So for the general case we have:

`y=5x^2+2x-6`
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

the process of completing the square introduces an error. It ads a term to the original equation. Thus this term must be removed. This is achieved by introducing a correction.

Let `k` be the correction value.

`color(blue)("Step 1")`

write as:`" "y=5(x^2+2/5x)-6`

Include the correction

`y=5(x^2+2/5x)-6+k`

At this stage `k=0` as we have not changed the overall values.
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
`color(blue)("Step 2")`

Move the power from `x^2` to outside the brackets

`y=5(x+2/5x)^2-6+k larr" now "k" starts to have a value"`
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
`color(blue)("Step 3")`

Remove the `x` from `2/5x`

`y=5(x+2/5)^2-6+k`
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
`color(blue)("Step 4")`

Halve the `2/5`

`y=5(x+2/10)^2-6+k`
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
This is the point where we find the value of `k`
The error comes from: `5(2/10)^2`. This is an added term and needs to be removed.

So `5(2/10)^2+k=0`

`=>color(red)(k=-(5xx4)/100" "=" "-20/100" " =" " -1/5)`

So we now have:

`y=5(x+2/10)^2-6color(red)(-1/5)`

`color(white)(2/2)`

`" "color(blue)(ul(bar(|color(white)(2/2)y=5(x+2/10)^2-31/5color(white)(2/2)|)))`
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Set `y=0` then we have

`+31/25=(x+2/10)^2`

`=>x+2/10=+-sqrt(31/25)`

`=>x=-2/10+-sqrt(31/25)`

`=>x=-2/10+-sqrt(31)/5`

`x=-1.313` to 3 decimal places

`x=+0.914` to 3 decimal places