How do you solve #(2x)/ (x+2) - 2 = (x-8) / (x-2)#?
2 Answers
I would find a common denominator and then solve for
Explanation:
Have a look:
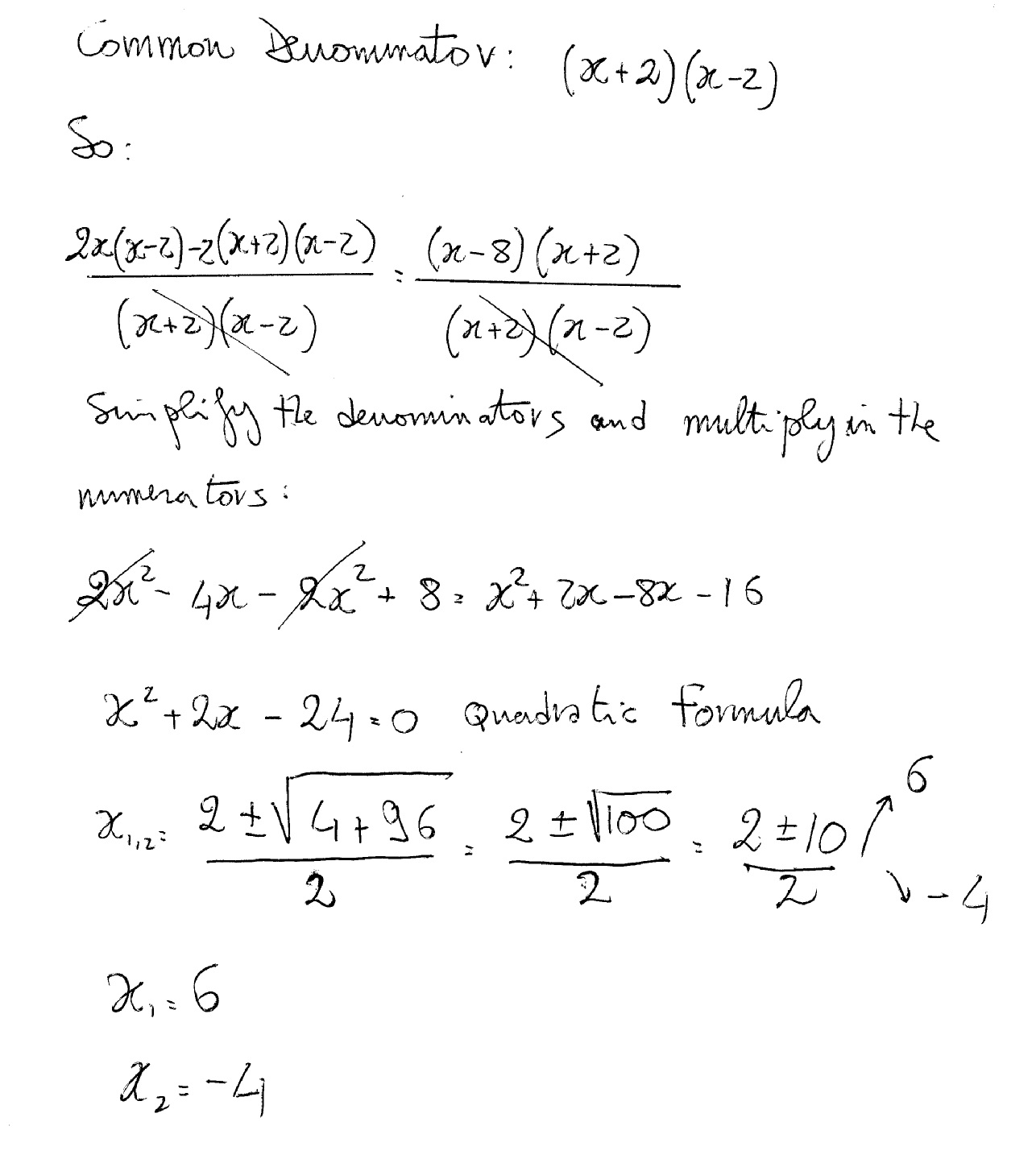
Multiply through by
Explanation:
Given:
Multiply both sides by
Note that when we multiply by
Multiplying out:
Add
To get this factorization, I looked for a pair of factors of
Since


