How do you solve #-3x^2 - 5 = 22#?
2 Answers
How do you solve
Explanation:
Since there is no "linear" term, that is a term with an "x" variable that is not squared, I would isolate the "
Take the square root of both sides:
And don't forget the
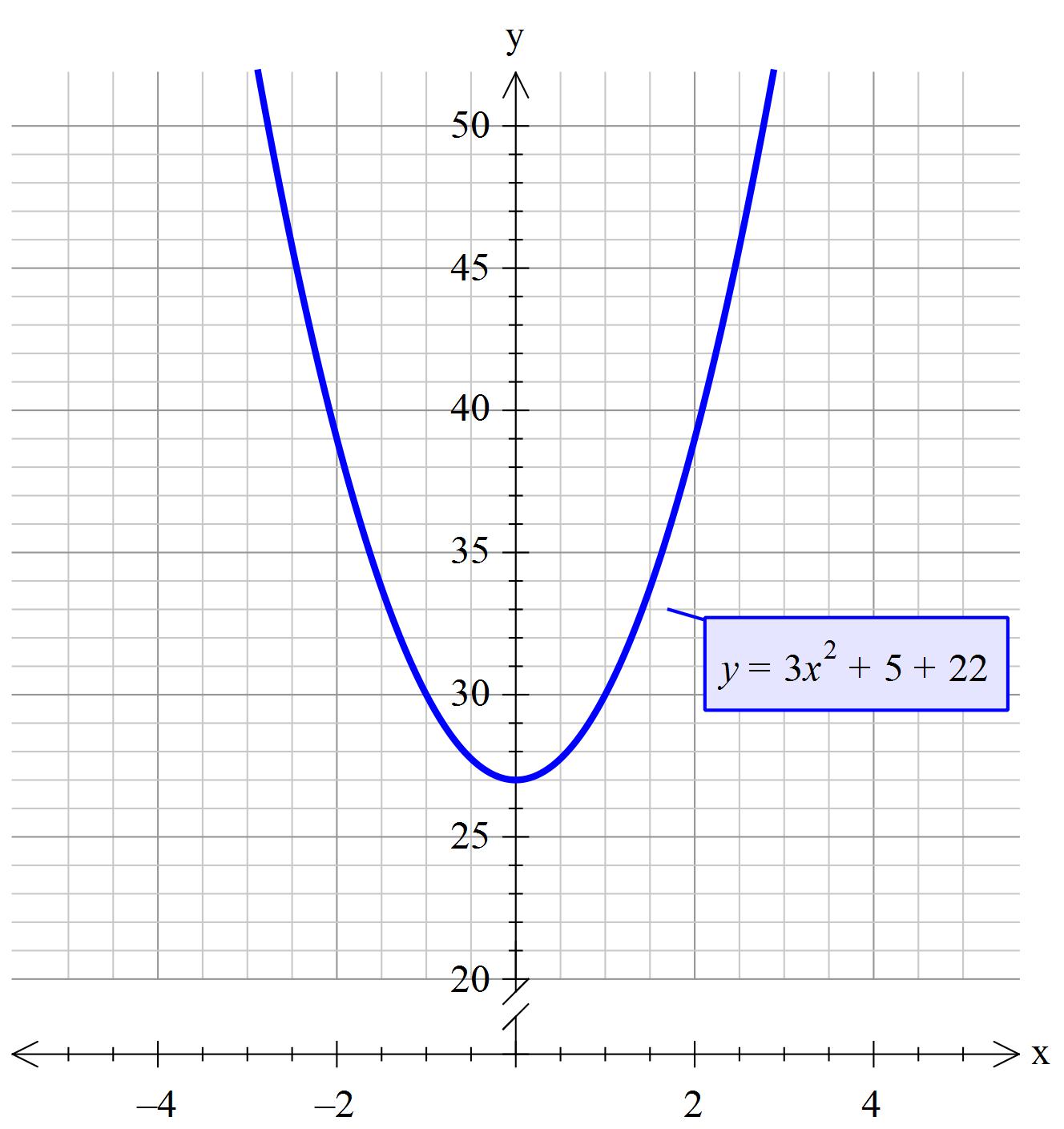
That is, there are no real solutions!
Graphically, this means that the function graph of f(x) =
I have taken you to a point where you can take over.
Explanation:
It is a matter of looking at whole number factors of the
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Add
Whole number factors of 22 can only be 2 and 11
Whole number factors of 3 can only be 3 and 1
Starting point. We know we have:
Considering combinations for the constant of 11
Try this one:
Try this one:
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
standard form
and
As soon as you see that there is a square root of a negative number then the curve does not cross the x-axis. Consequently there is no solution where
Thus the only solutions are for
I will let you finish this off.
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~