Question

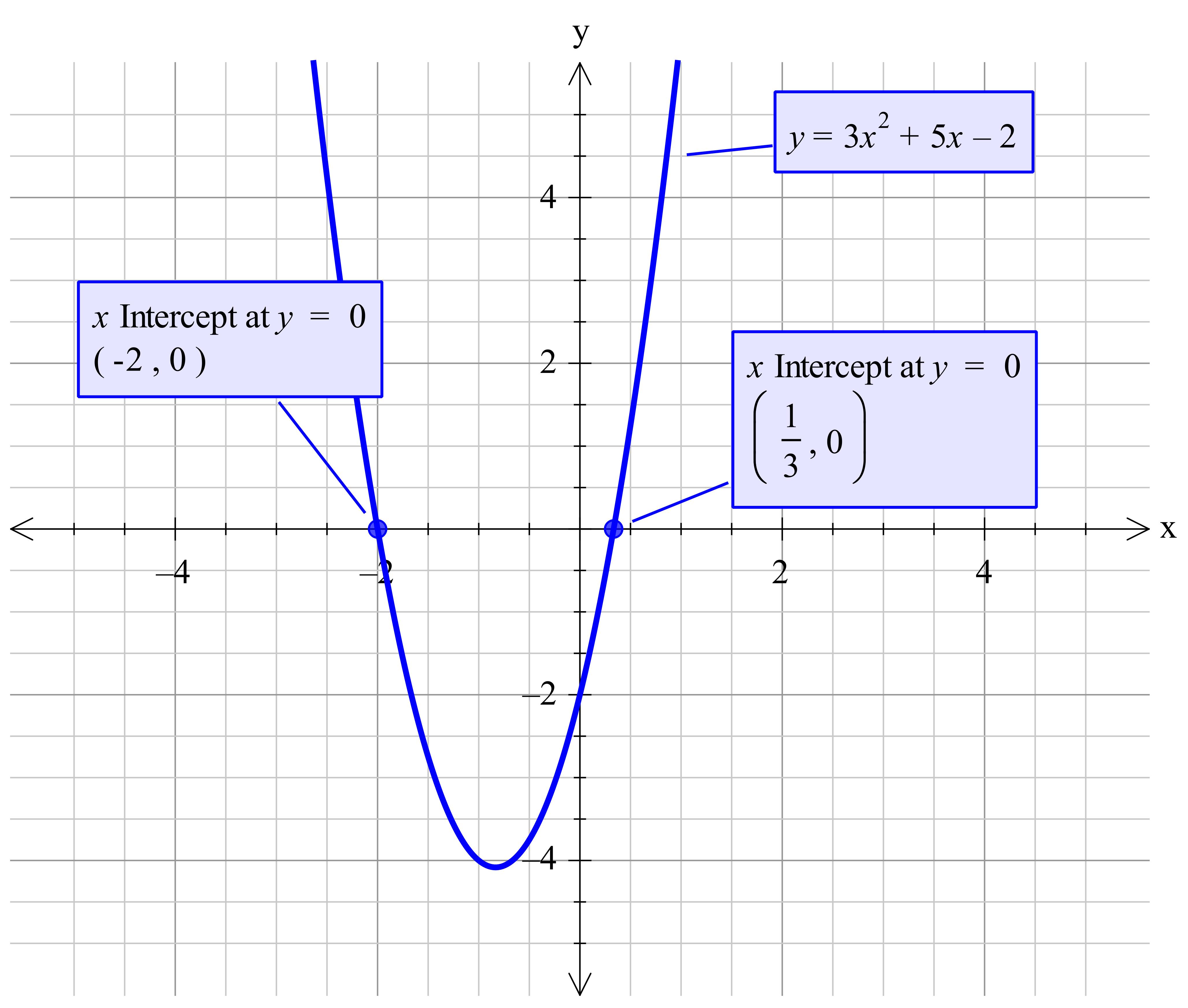
How do you solve `3x^2+5x-2=0`?

Answer 1

`x = -2 or x = 1/3`

Explanation:

Factorise to get `(3x - 1)(x + 2) = 0`

hence
`3x - 1 = 0 or x + 2 = 0`

giving
`x = 1/3 or x = -2`

Answer 2

`x = 1/3 or x = -2`

Explanation:

Find factors of 3 and 2 which subtract to make 5.

We should realise that (3x2) - 1 = 5.
Find the cross products and subtract to get 5.

`3" "1 " "rArr 1xx1 =1`
`1" "2" "rArr 3xx2 = 6 " "(6-1 = 5)`

Add in the signs.

`3" "-1 " "rArr 1xx-1 =-1`
`1" "+2" "rArr 3xx+2 = +6 " "(+6-1 = +5)`

`(3x-1)(x+2) = 0`
One of the factors must be 0.

If `3x-1 = 0, " then " x = 1/3`
If `x+2 = 0, " then " x = -2`

Answer 3

There is only one way to deal with factorization. That is lots of practice.
`x=+1/3`

`x=-2`

Explanation:

Given:`" "3x^2+5x-2=0`
'............................................................................................................

Both 3 and 2 are prime numbers so they can only be the products of:

for 2`->1xx2`
for 3`->1xx3`

So without taking any notice of the signs (sorted out afterwards) we have something like: `color(red)((3x+1)(x+2) " or "(3x+2)(x+1))`
I have kept both `3x" and "x` positive.

`color(red)("Note that the signs in the above will be wrong!")`

`color(green)("Ok. Lets consider the signs by looking at the "+5x)` `color(green)("from "3x^2+5x-2)`

Notice that
`(+3x)xx(+2)=6x`
`(-1)xx x=-x`

giving `6x-x=+5x` as required

So the factor form is very likely:

`(3x-1)(x+2)`

'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Check:
Multiplying out the brackets
`color(blue)((3x-1))color(brown)((x+2) )" "rarr" " color(brown)(color(blue)(3x)(x+2)color(blue)(" "-1)(x+2))`

`" "=3x^2+6x" "-x-2`

`=3x^2+5x-2` as required
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
So we have:

`3x^2+5x-2=0" "->" "(3x-1)(x+2)=0`

Note that anything `xx0=0`

This means that the solution is such that

`(3x-1)=0 -> x=+1/3`

`(x+2)=0->x=-2`