Question

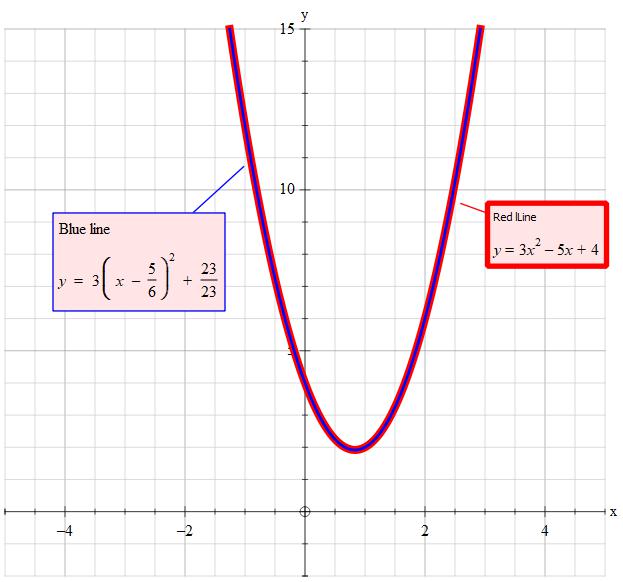
How do you solve `3x^2 - 5x+4=0` by completing the square?

Answer 1

`3(x-5/6)^2+23/12`

Explanation:

`3x^2-5x+4`
`3(x^2-5/3x+4/3)`
`3((x-5/6)^2-(5/6)^2+4/3)`
`3(x-5/6)^2-3(5/6)^2+4`
`3(x-5/6)^2-25/12+4`
`3(x-5/6)^2+23/12`

I double checked and worked backwards and gives you the original function. I knew I was working with fractions the minute I saw the `3x^2` which I didn't mind, as long as you prioritise the `3x^2` and turn that into `x^2` by itself so that completing the square would be easier.

Answer 2

`x=5/6+-sqrt(23)/6 i`

Explanation:

Write as:

`3(x^2-5/3x)+4=0" "................Equation(1)`

The next step introduces a value that is not in the original equation. We get rid of it by introducing the the as yet unknown value `k`. We will use this to turn the introduced value into 0

`color(green)(color(white)("dd.d")3(x^2-5/3x)+4=0)`
`color(white)("ddddd.dddd")darr`

`"halve the " -5/3`

`color(white)("ddddd.dddd")darr`
`color(green)(color(white)("ddd.d")3(x-5/6)^2+k+4=0)" ".............Equation(2)`
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
The introduced value is `3(-5/6)^2` so:

Set: `3(-5/6)^2+k=0` giving

`3(+25/36)+k=0`

`25/12+k=0color(white)("d")=>color(white)("d")k=-25/12" "......Equation(3)`
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Substitute `Eqn(3)` into `Eqn(2)`

`3(x-5/6)^2-25/12+4=0`

`3(x-5/6)^2+23/12=0`

`(x-5/6)^2=-23/36`

`x-5/6=+-sqrt(-23/36)`

`x=5/6+-sqrt(23)/6 i`