How do you solve #4cos^2x-1=0#?
1 Answer
Oct 21, 2016
Explanation:
This is a trivial quadratic equation in
In order to solve this you need to be familiar with the graphs of the trig functions along with common values:
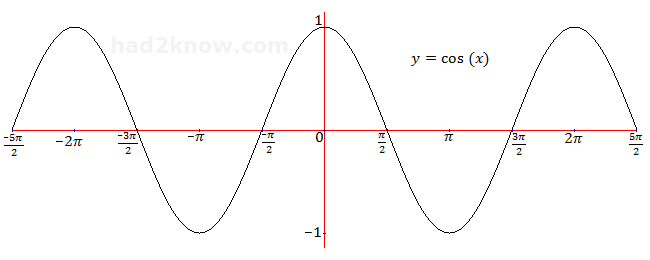
The range of soutions is not specified in the question, so lets assume we want a solutio in radians, and
Consider,
Consider,
So the solutions are:

