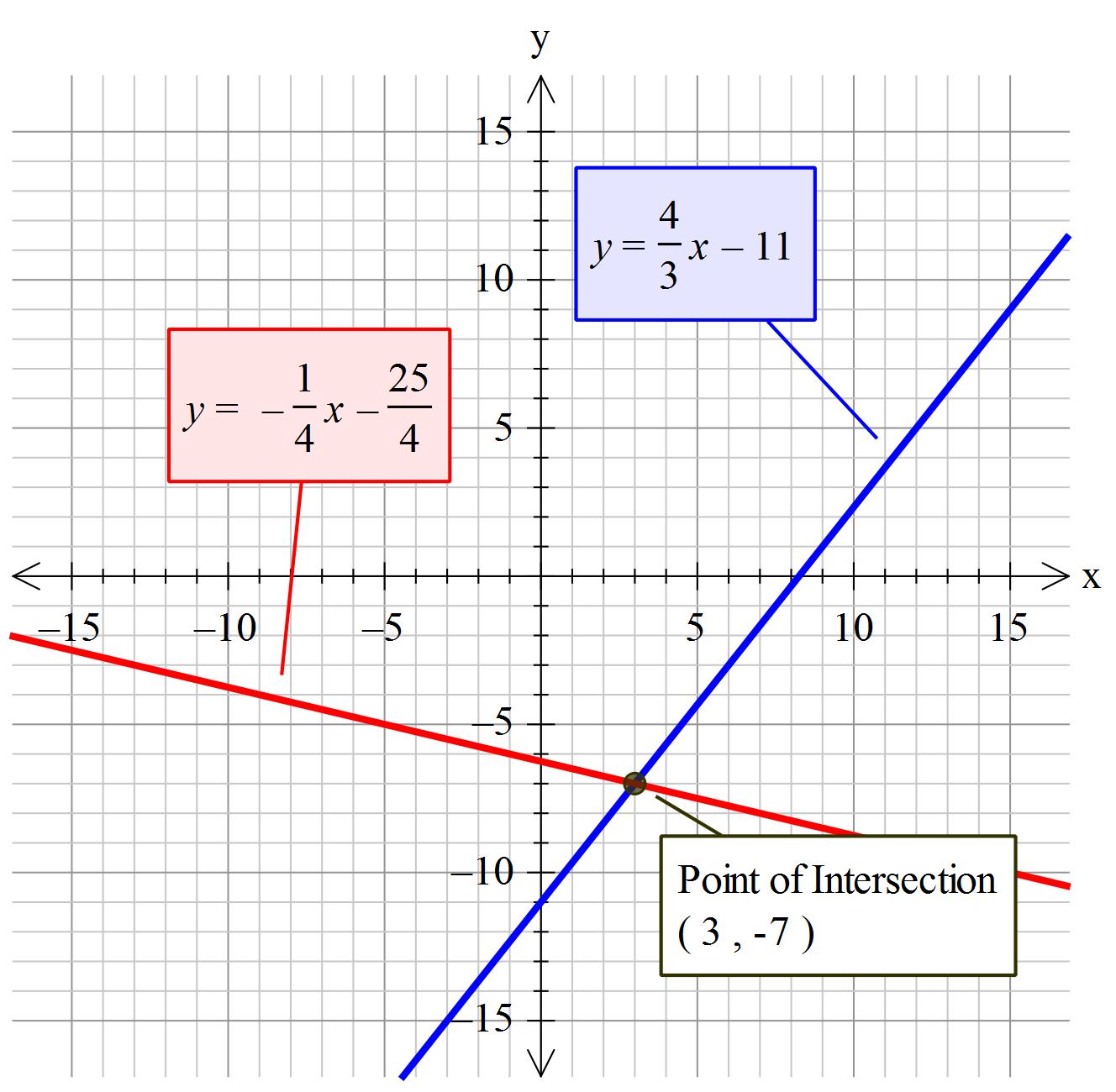
How do you solve 4x - 3y = 33 and x = - 4y - 25?
1 Answer
Point of intersection (lines cross)
Explanation:
Given:
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Using equation (2) substitute for
Multiply both sides by (-1)
Subtract 100 from both sides
Divide both sides by 19
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Substitute the value of
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~