Question

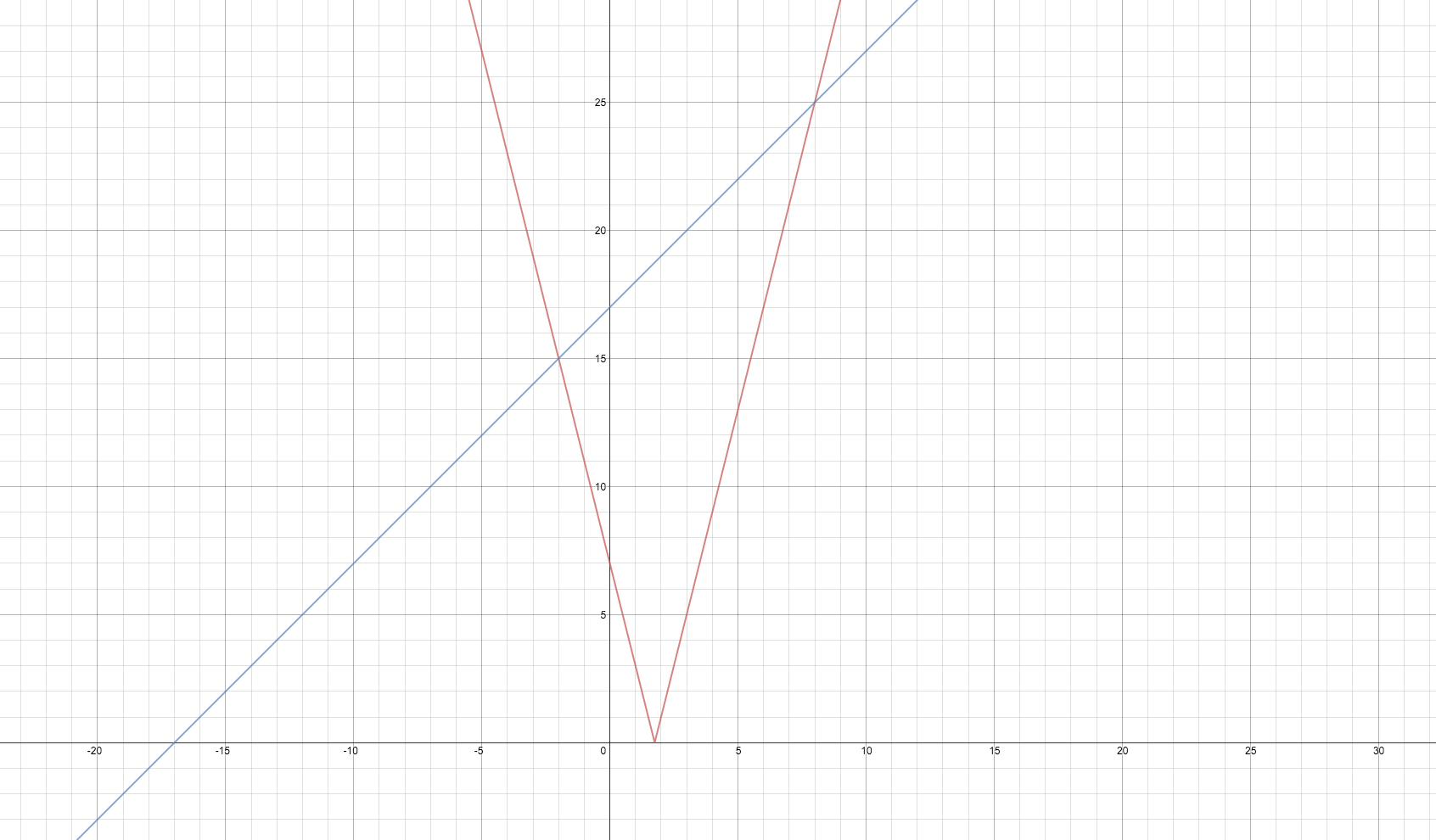
How do you solve `|-4x +7| = x + 17`?

Answer 1

`x=-2,8`

Explanation:

`1`. Recall that the absolute value equality property, `|a|=b`, can be written as `a=+-b`. Thus, there will be two solutions.

`|-4x+7|=x+17color(white)(X),color(white)(X)"gives:"`

`-4x+7=x+17color(white)(XX)color(purple)("or")color(white)(XX)-4x+7=-(x+17)`

`2`. For each equation, solve for `x`.

`color(white)(XXXx)-5x=10color(white)(XX)color(purple)("or")color(white)(XX)-4x+7=-x-17`

`color(white)(XXXXX)x=10/-5color(white)(XXXXx)-3x=-24`

`color(white)(XXXx)color(green)(|bar(ul(color(white)(a/a)x=-2color(white)(a/a)|)))color(white)(XXXx)x=(-24)/(-3)`

`color(white)(XXXXXXXXXXXXxx)color(green)(|bar(ul(color(white)(a/a)x=8color(white)(a/a)|)))`

If you graph the equation, you can see that the intersection points occur when `x=-2` and `x=8`:

`:.`, `x=-2` or `8`.