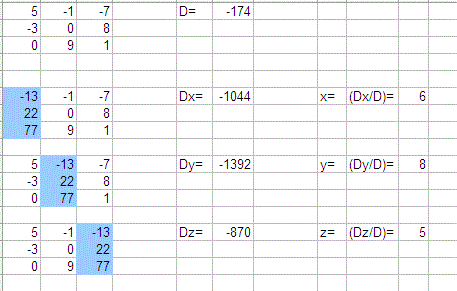The given equations could be written in matrix form as:
#((x,y,z,"|",c),(5,-1,-7,"|",-13),(-3,0,8,"|",22),(0,9,1,"|",77))#
#color(white)("XXX")#actually the top row shouldn't be there, but I though it might make the translation more clear.
Cramer's Rule says that if you take the derivatives:
#color(white)("XXX")D = # the matrix composed of the variable coefficients (the left side of the above)
#color(white)("XXX")D_x = # the matrix composed of the variable coefficients with the #x# column replaced with the #c# column.
#color(white)("XXX")D_y = # the matrix composed of the variable coefficients with the #y# column replaced with the #c# column.
#color(white)("XXX")D_z = # the matrix composed of the variable coefficients with the #z# column replaced with the #c# column.
then
#color(white)("XXX")x=|D_x|/|D|color(white)("XXX")y=|D_y|/|D|color(white)("XXX")z=|D_z|/|D|#
Here's what the solution looks like done on a spreadsheet: