How do you solve #-6 + |2x – 4| = -3#?

Question

1665 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-01-27T13:38:13

#x={1/2,7/2}#

Absolute value is the distance between a value and 0 on the number line
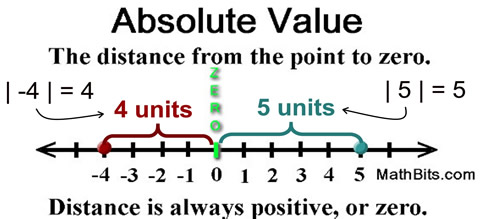
enter image source here
So, the distance should be always a positive integer

#-6+|\2x-4|=-3#

#|\2x-4|=6-3=3#

This equation is possible because the absolute value is a positive integer.

Assume 2 values:

#2x-4=3#

#2x-4=-3#

Solve for the first equation:

#2x-4=3#

#2x=3+4=7#

#2x=7#

#x=7/2#

So, the first value of #x# is #7/2#

Now solve for second equation:

#2x-4=-3#

#2x=4-3=1#

#2x=1#

#x=1/2#

So, #x={1/2,7/2}#