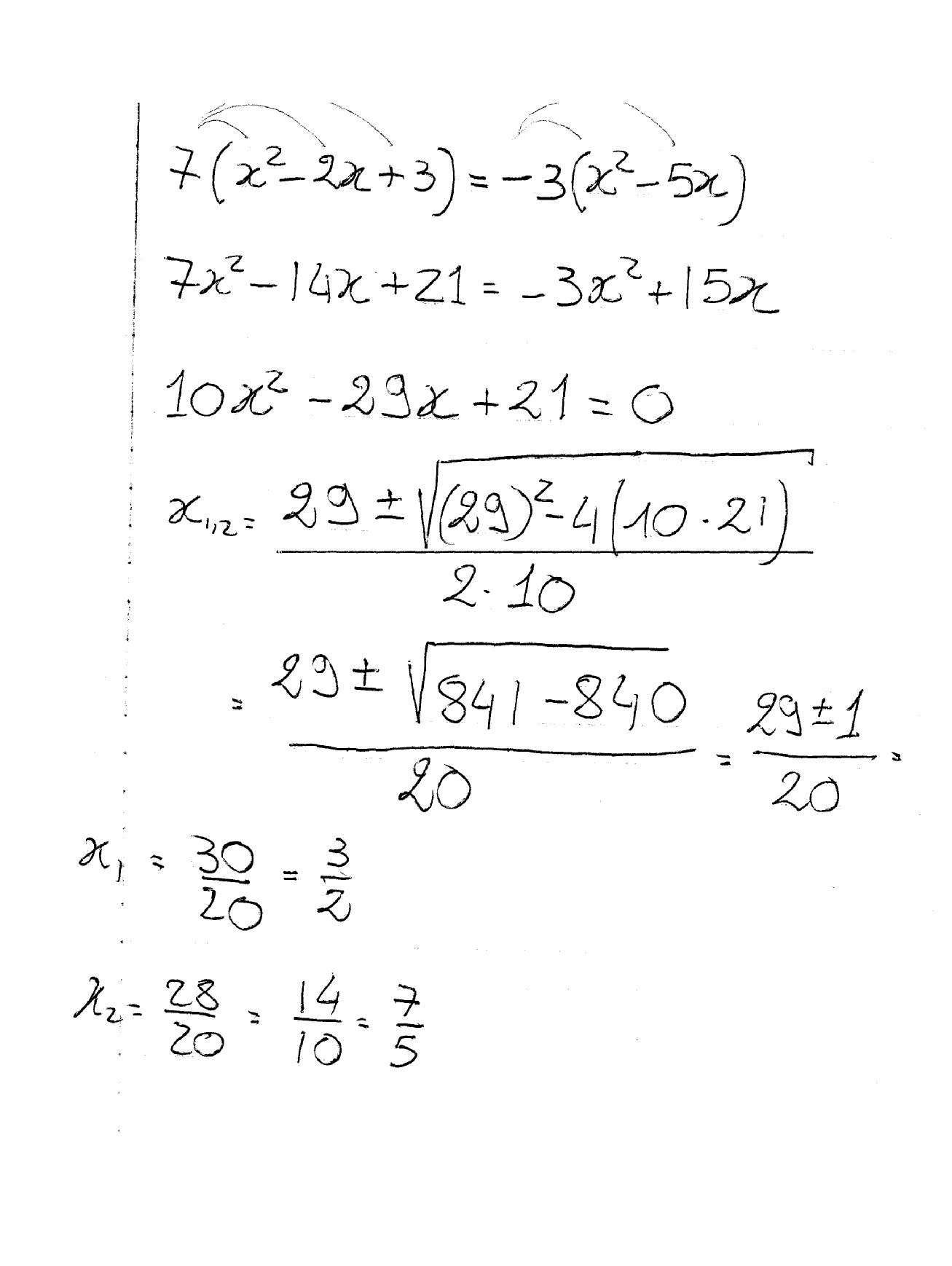How do you solve #7(x^2-2x+3) = -3(x^2-5x)#?
2 Answers
Mar 27, 2015
Let's do the multiplications at both sides:
Add
Subtract
So we have a quadratic equation of the form
Since
Since
So,
Mar 27, 2015
Have a look: