How do you solve #|-7x + 7| = 14#?
2 Answers
Explanation:
or
or
or
or
Now consider
or
or
or
or
or
Explanation:
Remember that everything inside the two | | is read as positive. This is called an 'absolute' value
Written as in the question or as 'abs(-7x+7)=14'
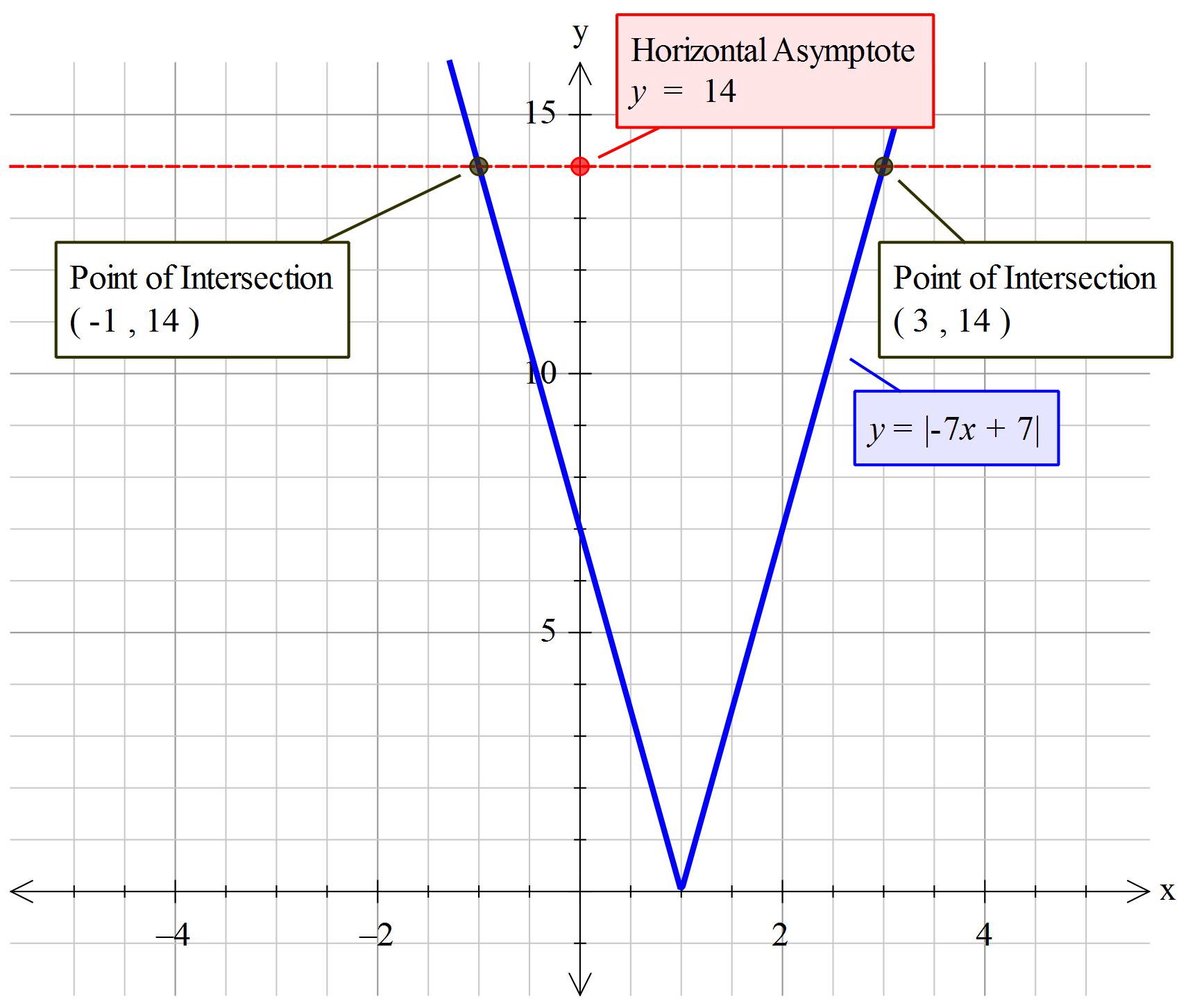
The part of the equation inside the | | may be positive or negative but will always be read as a final positive overall value.
Thus what is inside the | | has the possibility to be -14 or +14 and still satisfy the equation
Suppose
Suppose

