Question

How do you solve `8x^2 + 14x + 5 = 0` by completing the square?

Answer 1

`x=-5/4" or "x=-1/2`

Explanation:

`"using the method of "color(blue)"completing the square"`

`• " the coefficient of the "x^2" term must be 1"`

`"factor out 8"`

`rArr8(x^2+7/4x+5/8)=0`

`• "add/subtract "(1/2"coefficient of the x-term")^2" to"`
`x^2+7/4x`

`8(x^2+2(7/8)xcolor(red)(+49/64)color(red)(-49/64)+5/8)=0`

`rArr8(x+7/8)^2+8(-49/64+5/8)=0`

`rArr8(x+7/8)^2-9/8=0`

`rArr8(x+7/8)^2=9/8`

`"divide both sides by 8"`

`rArr(x+7/8)^2=9/64`

`color(blue)"take the square root of both sides"`

`sqrt((x+7/8)^2)=+-sqrt(9/64)larrcolor(blue)"note plus or minus"`

`rArrx+7/8=+-3/8`

`"subtract "7/8" from both sides"`

`rArrx=-7/8+-3/8`

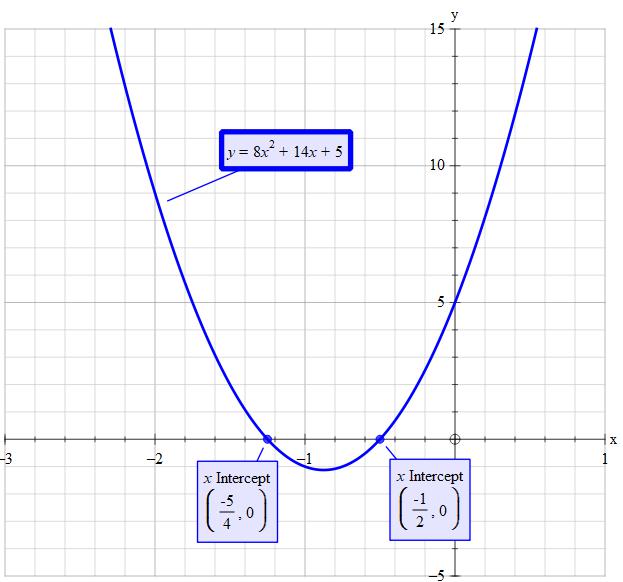
`rArrx=-7/8-3/8=-10/8=-5/4`

`"or "x=-7/8+3/8=-4/8=-1/2`

Answer 2

`x= -10/8=-5/4`
`x=-4/8=-1/2`

Explanation:

Given: `color(green)(y=0=8x^2+14x+5)`

Write as:
`color(green)(0=8(x^2+14/8x)+5 color(white)("ddd")->color(white)("ddd")0=8(x^2+7/4x)+5)`

The 'perfect' square related to `x^2+7/4x " is " (x+7/8)^2`

but `8(x+7/8)^2` introduces the value of `color(red)(8xx(7/8)^2)` that is not in the original equation. We put it in so we have to take it out.

`color(green)(0=8(x^2+7/4x)+5 )`

`color(green)(0= 8(x+7/8)^2color(red)(-[8xx(7/8)^2 ] )+5 )`

`color(green)(0=8(x+7/8)^2-9/8 )`
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
`color(blue)("Check")`

`8(x+7/8)^2-9/8`
`8(x^2+7/4x +49/64)-9/8`

`8x^2+14x+49/8-9/8`

`8x^2+14x +40/8`

`8x^2+14x+5` as required!
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
`color(green)(0=8(x+7/8)^2-9/8color(white)("dd") ->color(white)("dd")+9/8=8(x+7/8)^2`

`color(green)( color(white)("ddddddddddddddddddd")->color(white)("dddd") 9/64=(x+7/8)^2)`

`color(green)(color(white)("ddddddddddddddddddd")->color(white)("d.d")+-3/8=color(white)("d")x+7/8)`

`color(green)(color(white)("ddddddddddddddddddd")->color(white)("ddd.dd")x=-7/8+-3/8)`

`x= -10/8=-5/4`
`x=-4/8=-1/2`

Answer 3

`x=-1/2 or x=-5/4`

Explanation:

We have,

`8x^2+14x+5=0`

`=>8x^2+14x=-5`

`=>8x^2+14x+K=K-5...to(A)`

Now we have to find `K`,such that,`(8x^2+14x+K)`is a square.

Here,

`I^(st)term=8x^2`

`II^(nd) term=14x`

`III^(rd)term=K`

Formula for `color(red)(III^(rd)term=(II^(nd)term)^2/(4xxI^(st)term)...to(psi)`

`i.e. K=(14x)^2/(4xx8x^2)=(196x^2)/(32x^2)=49/8`

So,from`(A)`,we get

`8x^2+14x+49/8=49/8-5`

`(sqrt8x)^2+2(sqrt8x)(7/sqrt8)+(7/sqrt8)^2=9/8`

`(sqrt8x+7/sqrt8)^2=(3/sqrt8)^2`

`=>sqrt8x+7/sqrt8=+-3/sqrt8`

`=>8x+7=+-3`

`=>8x+7=3 or 8x+7=-3`

`=>8x=3-7 or 8x=-3-7`

`=>8x=-4 or 8x=-10`

`=>x=-1/2 or x=-5/4`

`=>x=-0.5 or x=-1.25`

Note: Formula `color(red)((psi)` for `color(red)(III^(rd)term`, is always true.