How do you solve #abs(20+1/2x)>6#?
2 Answers
See a solution process below:
Explanation:
The absolute value function takes any term and transforms it to its non-negative form. Therefore, we must solve the term within the absolute value function for both its negative and positive equivalent.
Or
Or, in interval notation:
Explanation:
One way to approach the evaluation of an absolute value inequality like
For example if we let
Presented on the number line this would look like:
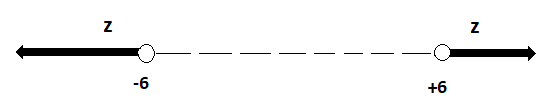
That is
then since we know
these become

