Question

How do you solve `abs(x^2-2x-3) = sqrt (2- lnx)`?

Answer 1

`x = {2.73282,3.21631}`

Explanation:

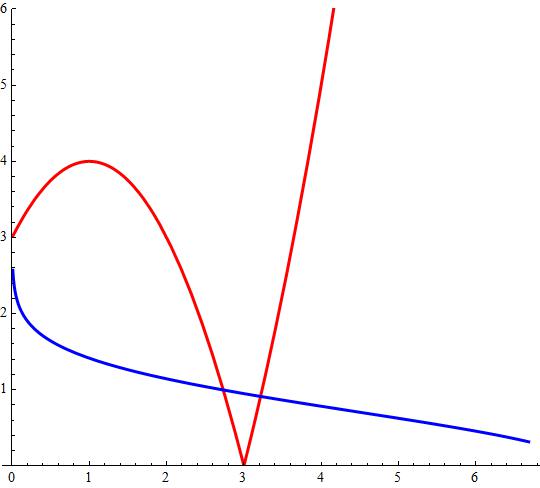
The best way to solve this equation is using an iterative method, after knowing the initial trials. The initial iterations can be found after plotting the curves

`y_1 = abs(x^2-2x-3)` and
`y_2 = sqrt (2- lnx)`

this plot will cover the interval `0 < x < e^2` because in this interval we have feasible solutions.

We now will perform a series of algebraic transformations into the original problem, in order to remove handling difficulties.

First after squaring both equation terms, we consider

`abs(x^2-2x-3)^2= 2- log_ex`

and now we call

`f(x) = (x^2-2x-3)^2-2+log_e x = 0`

Supposing we know an initial guess `x_0` we can proceed using the Taylor series first approximation

`f(x_{k+1}) = f(x_k) + f'(x_k)(x_{k+1}-x_k) + O^2(x_k)`

but we need that `f(x_{k+1})= 0` then, supposing `O^2(x_k)` small enough, we obtain

`x_{k+1} = x_k - f(x_k)/(f'(x_k))`

From the plot we propose first `x_0=2`
and obtain successively
`x_1 = 2.66897`
`x_2 =2.72804`
`x_3 =2.73279`
`x_4 =2.73282`

and also `x_0 = 4`
obtaining successively
`x_1 = 3.59525`
`x_2 =3.35944`
`x_3 =3.24893`
`x_4 =3.21869`
`x_5 =3.21632`
`x_6 =3.21631`

This way we obtained the equation solution within 6 sd!

Attached a plot with `y_1` in red and `y_2` in blue, showing the two solutions.