How do you solve and find the value of #cos(tan^-1sqrt3)#?
1 Answer
Dec 27, 2016
Explanation:
The standard definition of the inverse tan function implies an angle either Quadrant I or II.
The angle
By the Pythagorean Theorem this implies a hypotenuse of
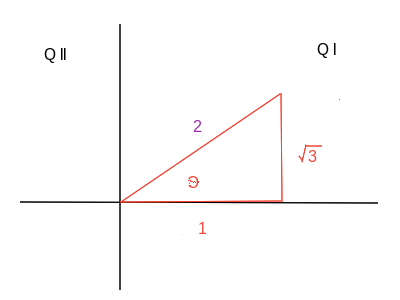
Using this triangle and the definition of
we have
