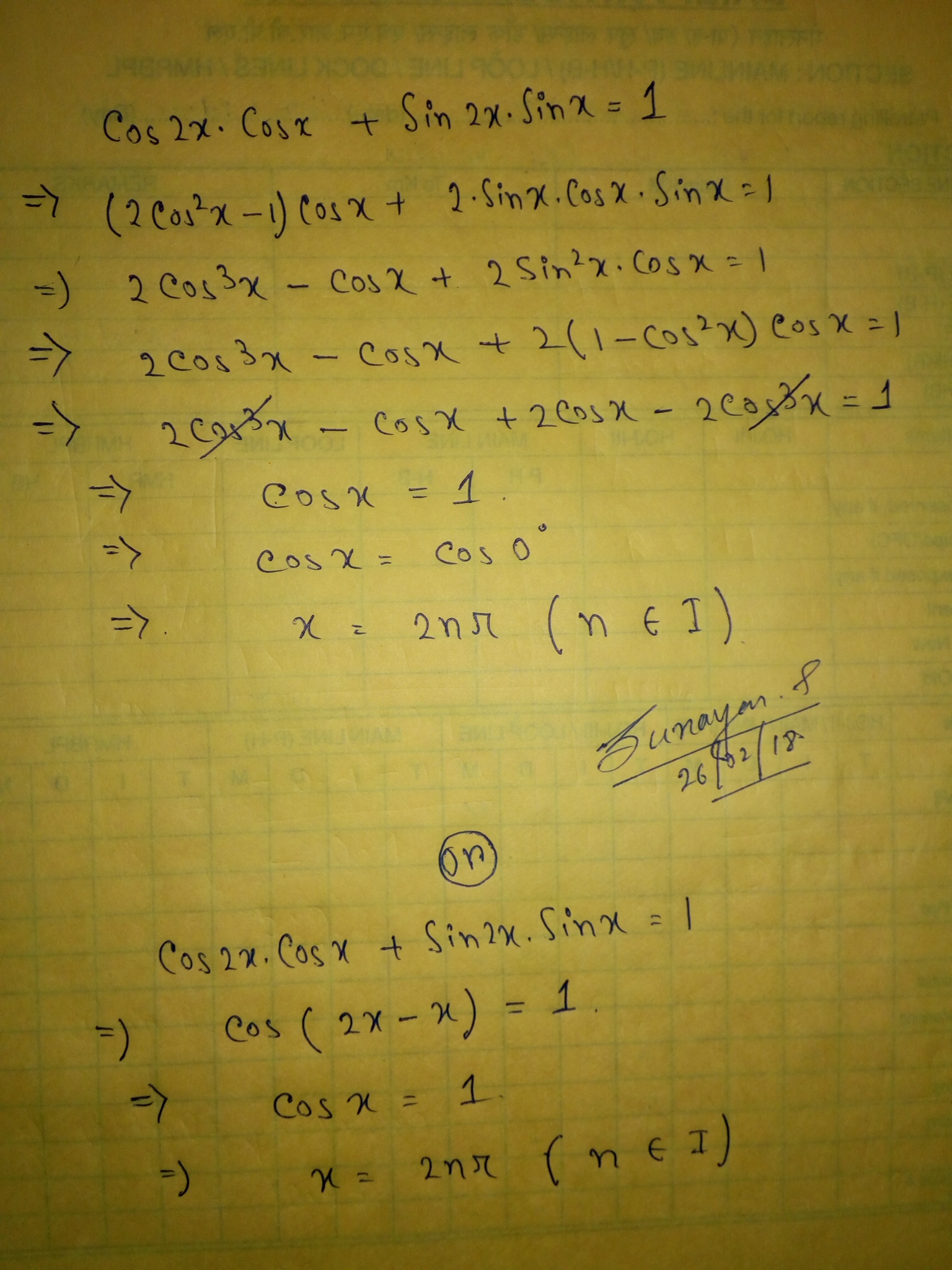First, we want everything in this equation to be in the form of one trigonometric function. Let's have everything in the form of #cos(x)#.
Recall the following identity:
#sin(2x)=2sin(x)cos(x)#
Rewrite with this applied:
#cos(2x)cos(x)+2sin(x)cos(x)sin(x)=1#
#cos(2x)cos(x)+2cos(x)sin^2(x)=1#
Recall that
#sin^2(x)+cos^2(x)=1#
Solving for #sin^2(x)# gives
#sin^2(x)=1-cos^2(x)#
Apply this to the instance of #sin^2(x)# in the equation:
#cos(2x)cos(x)+2cos(x)(1-cos^2(x))=1#
Distribute #2cos(x)# through:
#cos(2x)cos(x)+2cos(x)-2cos^3(x)=1#
Recall the following identity:
#cos(2x)=2cos^2(x)-1# (There are three ways to write the double-angle identity for #cos(2x)#; however, we only want the one where everything is in terms of #cos(x)#)
Apply:
#(2cos^2(x)-1)cos(x)+2cos(x)-2cos^3(x)=1#
Multiply #cos(x)# through and simplify:
#cancel(2cos^3(x))-cos(x)+2cos(x)-cancel(2cos^3(x))=1#
Now, we have a very simple equation to solve:
#cos(x)=1#
We want all values of #x# for which #cos(x)=1#.
#cos(x)=1# for #x=2pin# where n is any integer. We must include #n# because the period of #cos(x)# is #2pi#, meaning that any value of #cos(x)# repeats every #2pi# units (regardless of whether we add or subtract #2pi#). #cos(0)=1#, but so does #cos(2pi), cos(4pi), cos(-2pi)#, and infinitely many other values obtained; therefore, we account for these with #2pin.#