How do you solve for x: in #2^x + 2^-x = 5/2#?
1 Answer
May 14, 2016
Explanation:
(I'm hoping that someone will come up with a better method of solving, since the following is simply "solution by observation").
We are told:
Observe that
So
which implies
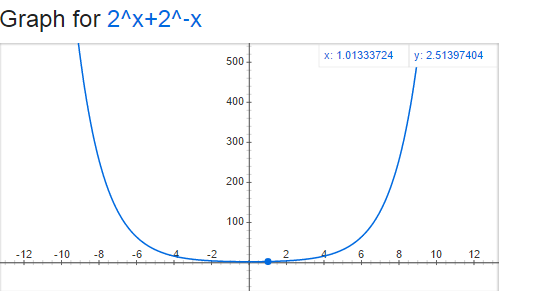
Graph
Another possible way is looking at a graph