How do you solve #ln(x) = x^3 - 3#?
1 Answer
Explanation:
We have:
# lnx=x^3-3 #
This equation cannot be solved analytically, so first we graph the functions to get a "feel" for the solutions:
So, we establish that there are two solutions, approximately
# x = g(x) # and use an iteration#x_(n+1) = g(x_n) #
There will many functions,
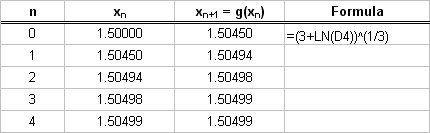
Root 1: For
We could try:
# lnx = x^3-3 => x^3=3+lnx#
# :. x = root(3)(3+lnx) #
So we will try the iterative equation:
# x_0 \ \ \ \ = 1.5 #
# x_(n+1) = root(3)(3+lnx_n)#
Using excel we can quickly process the iterative equation to any degree of accuracy. Here we work to 5dp:
Put
As it happens, and attempt of using
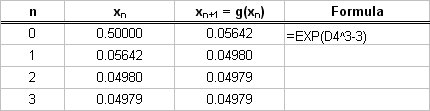
Root 2: For
# lnx = x^3-3 => x = e^(x^3-3) #
So we will try the iterative equation:
# x_0 \ \ \ \ = 0.5 #
# x_(n+1) = e^((x_n)^3-3) #