How do you solve rational expressions by multiplying by the least common multiple?
1 Answer
The least common multiple helps you to deal with expressions in which you must add or subtract fractions.
There are mnemonic rules to deal with this but I like to "see" the problem...
Imagine that you are out eating a pizza with some friends (3 for example). If your pizza comes divided in 4 slices it is ok...you can add 2 of them together and...presto...you have half pizza!!!
But if you start to cut one of the slices in half (someone is on a diet) and make another bigger (someone is not on a diet) the thing gets complicated...If you add two slices again you may find that you have a thin slice plus a big slice and...what part of the entire pizza you get? You do not know...!!!!
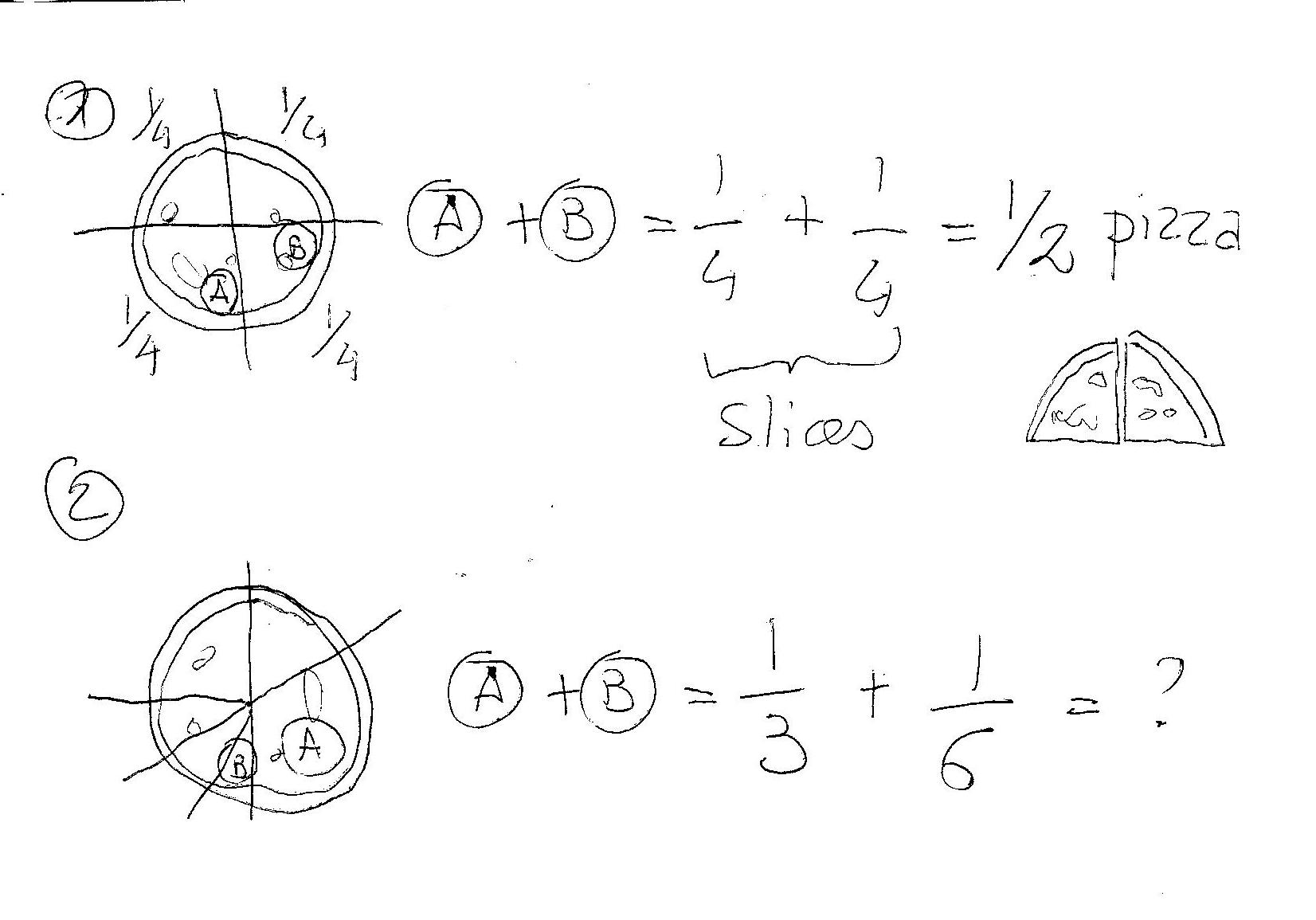
With fractions is the same...it is better to have equal slices to add them together!!!
In case 1 you can add together immediately the numerators because the denominators are equals (slices of same size!). And you get:
In case 2 first you need to make the slices of the same "size". To do that you use a common size (the least common multiple) and you "resize" all your slices according to this size.
You have:
You have:
Multiples of
Multiples of
The least common multiple is
Now you have:
Note that this work with subtraction as well!!!

