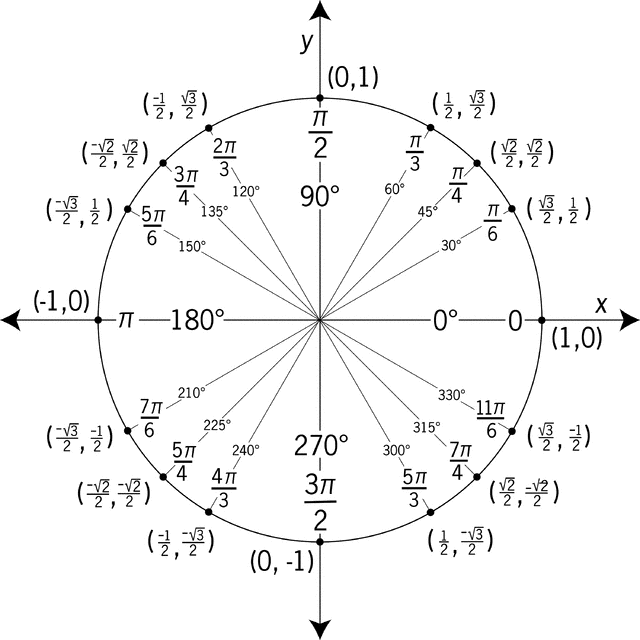
How do you solve tan^2x/secx+cosx=2 for 0<=x<=2pi?
1 Answer
Apr 19, 2018
Explanation:
First, recalling that
Add the expressions, using
Recall that
Invert both sides:
In the interval
First, recalling that
Add the expressions, using
Recall that
Invert both sides:
In the interval
