Question

How do you solve the equation `3x^2+6x=2x^2+3x-4` by completing the square?

Answer 1

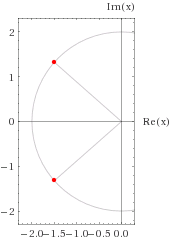
`x = -3/2 -sqrt(7)/2 \ i, -3/2 +sqrt(7)/2 \ i`

Explanation:

We have:

`3x^2+6x = 2x^2+3x-4`

First let us collect terms on the LHS

`3x^2 - 2x^2 + 6x - 3x -4 = 0`
`:. x^2 + 3x +4 = 0`

Now we complete the square, by forming a term with half the "`b`" value; that is

`:. (x + 3/2)^2 - (3/2)^2 +4 = 0`
`:. (x + 3/2)^2 - 9/4 +4 = 0`

Which we can now re-arrange and solve;

`:. (x + 3/2)^2 = -7/4`

`:. x + 3/2 = +-sqrt(7)/2 \ i`

`:. x = -3/2 +-sqrt(7)/2 \ i`

Leading to the two complex conjugate solutions:

`x = -3/2 -sqrt(7)/2 \ i, -3/2 +sqrt(7)/2 \ i`