How do you solve the inequality #abs(3x-4)<20#?
2 Answers
Jan 19, 2016
Explanation:
Removing the abs the equation became:
This is equivalent to the follow system:
Drawing the inequality system graph we have to pick up the
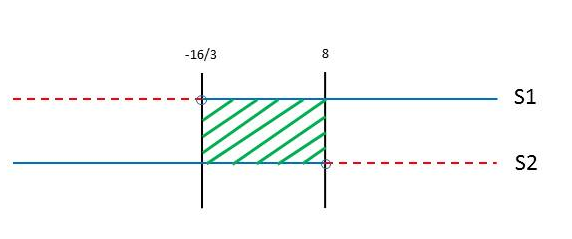
Jan 26, 2016
(-16/3, 8)
Explanation:
In the second expression if we multiply both parcels by -1, we must invert the signal:
Now, we add 4 in both sides of the inequality:
Then we divide by 3
so the solution is the interval
(-16/3, 8)

