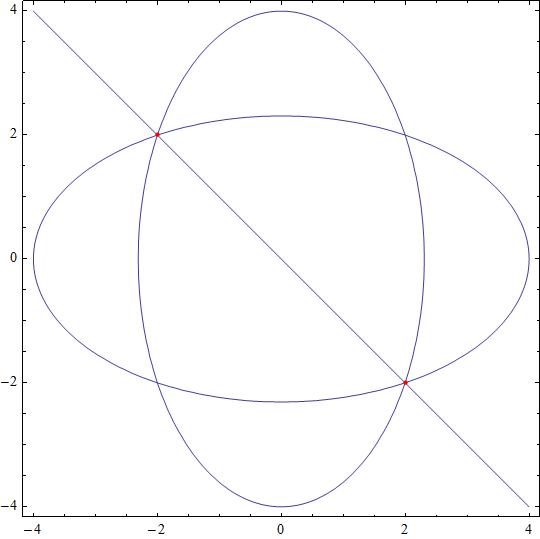
How do you solve the system #x^2+3y^2=16# and #3x^2+y^2=16# and #y=-x#?

Question

1568 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-07-10T11:45:13

#{x,y} = {2,-2}# or #{x,y} = {-2,2}#

Three equations and two incognitas. One of them must be redundant, to have a solution. Being a nonlinear system is not trivial to detect redundancy.

First we solve for #x_2 = x^2# and #y_2 = y^2# the system

#{ (x_2 + 3 y_2 = 16), (3 x_2 + y_2 = 16) :}#

giving

#x_2 = x^2 = 4# and #y_2 = y^2 = 4#

testing the solutions #x=pm2# and #y=pm2# in the last equation

#x+y=0#

we follow with the solution which is

#{x,y} = {2,-2}# or #{x,y} = {-2,2}#

enter image source here