Solving by Substitution
Key Questions
-
System of equations are written in the following format:
#2x + 4y = 16#
#6x - 3y = 18# x and y for variables are just examples. The goal is to line these up so that matching variables from each linear equation are under each other.
There are 3 ways to solve this:
1) Substitution Method
2) Elimination Method
3) Cramers Rule using Matrices.
Don S.
·
·
Sep 9 2014
-
I'm not sure where exactly you mean "final" in the solving process. So, I've prepared a couple of problems that I will work through slowly and carefully, showing all the steps to the final answer.
Example 1: Solve the following system of equations-
#2x + y = 5, 3x + 2y = 9# Since we want to solve with substitution, we must solve for one variable in one of the equations. I think it would be easiest to solve for
#y# in the first equation.#y = 5 - 2x# We can now substitute into the other equation:
#3x + 2(5 - 2x) = 9# #3x + 10 - 4x = 9# #-x = -1# #x = 1# We must now find the value of
#y# . This is found by inserting#x = 1# into one of the equations and solving for#y# .#y = 5 - 2x# #y = 5 - 2(1)# #y = 3# Hence, our solution set is
#{1, 3}# .Example 2: Find all real values of
#x# and#y# that satisfy the following system of equations:#3y = -2x^2 + 2, 2x^2 - 3y^2 = -4# Once again, as with the last example, we need to solve for one of the variables in one of the equations. It looks easiest to isolate the
#y# in the first equation, however solving this equation won't be as neat as solving the previous one.#y = -2/3x^2 + 2/3# We can now substitute into equation #2.
#2x^2 - 3(-2/3x^2 + 2/3)^2 = -4# #2x^2 - 3(4/9x^4 - 8/9x^2 + 4/9) = -4# #2x^2 - 4/3x^4 + 8/3x^2 -4/3 = -4# #-4/3x^4 +14/3x^2 + 8/3 = 0# Solve using a graphing calculator. If it's a standard one, like a TI84, use
#y_1 = -4/3x^4 + 14/3x^2 + 8/3 = 0# and#y_2 = 0# , and press "calc" followed by "intersect".This will give you real roots of
#2# and#-2# . All that is left to do is solve for#y# .#y = -2/3(2)^2 + 2/3" AND "-2/3(-2)^2 + 2/3# #y = -8/3 + 2/3" AND "-8/3 + 2/3# #y = -2" AND " -2# Hence, our solution set is
#{2, -2}# and#{-2, -2}# .Use the following practice exercises to develop your comfort with the skills dealt with in this answer.
Practice exercises:
- Find the real values of
#x# and#y# that satisfy the following systems of equations.
a)
#2x - 3y = 4, x + 2y = 9# b)
#3x + y = -2, x^2 = y# c)
#2x^2 - 3y^2 = -10, x^2 - 2x + 3y = 5# Hopefully this helps, and good luck!
Noah G
·
1
·
Aug 20 2016
- Find the real values of
-
With linear systems of equations, there are three possible outcomes in terms of number of solutions:
- One solution.
- Infinitely many solutions.
- No Solutions at all.
If there is one solution, it means that there is a single intersection between the two lines that your equations give. For example, considering the following equations:
#y = 2x#
#y = -x+9# If we graphed them both, this is what we'd end up with:
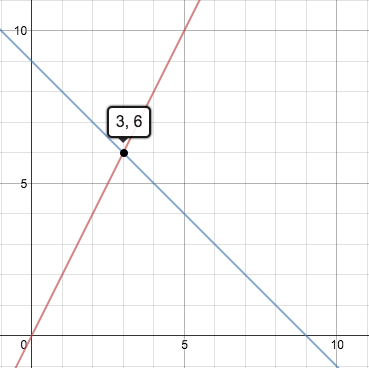
Blue line:
#y=-x+9#
Red line:#y=2x# As you can see, both lines intersect at the coordinate
#(3,6)# . This means that#(3,6)# is a solution to both equations, or in simpler terms, if you plugged in 3 for#x# in either equation, you would get 6 for#y# .If there are infinitely many solutions, it means that both your equations are referring to the same line . For example, if we took our graph from last time but made both lines
#y=2x# :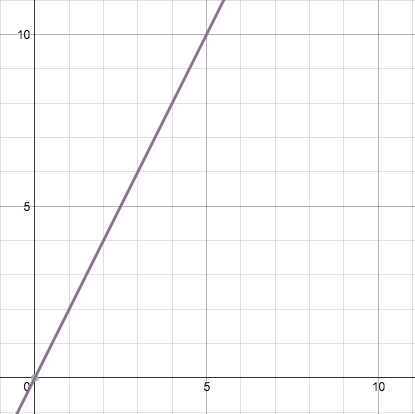
As you see, the two lines are indiscernible from one another. Hence we can say that they share ever single solution that is valid for them, or rather have infinitely many solutions that work for the both of them.
Lastly, if there are no solutions to a system, it means that the two lines represented by the equation are parallel.
For example, consider the following equations:
#y=3x# (blue)
#y=3x+4# (red)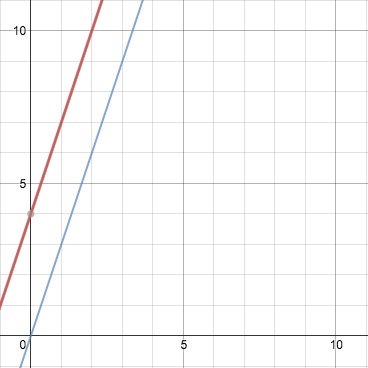
As you can see, the two lines are parallel, and will never meet. Therefore, they have no points in common, and therefore no common solutions . An easy way to check for parallel lines is to check if your two equations have the same slope, but different y intercepts.
Hope that helped :)
Darshan Senthil
·
·
Oct 22 2014
-
Answer:
Any set of equations is a system of equations.
Explanation:
See my answer to "How do you write a system of equations"
http://socratic.org/questions/how-do-you-write-a-system-of-equations
George C.
·
1
·
Jul 19 2015
-
I think that this is better explained with an example.
Lets say that we have the linear system
#x+y=17#
#x-y=3# Neither one of these equation can be solved on their own because an equation with more than one unknown value cannot be solved.
We have to eliminate one of the variable by substitution.
We have 2 options. First, pick one of equations and then solve for either
#x# or#y# .Lets use the first equation and solve for
#x# .#x+y=17# #x=17-y# Now we see that
#x# and the expression#17-y# are the same quantity. We will leverage this information with the second equation by replacing the#x# with#17-y# .#x-y=3 -># Second equationMake substitution for
#x# #(17-y)-y=3# Combine like terms
#17-y-y=3# #17-2y=3# Subtract 17 from both sides
#-2y=-14# Divide by sides by
#-2# #(-2y)/(-2)=(-14)/(-2)# #y=7# Now we can find
#x# by substituting in the#7# for#y# .#x+7=17#
#x=10# Okay, so now we know that
#y=7# and#x=10# .We check our work by substituting those values into the other equation.
#x-y=3#
#10-7=3#
#3=3 -># We are correct
AJ Speller
·
·
Sep 21 2014