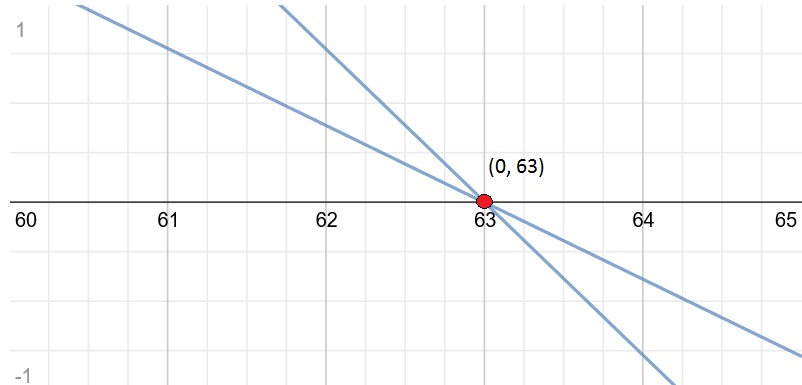
How do you solve using the addition method and determine if the system is independant, dependant, inconsistant given 3/7x+5/9y=27 and 1/9x+2/7y=7?
1 Answer
Feb 6, 2017
Explanation:
The system of equations is
Multiply the first equation by
This gives
Adding them together gives
Plug
If the lines intersect, then the system has one solution, given by the point of intersection. The system is consistent and the equations are independent.