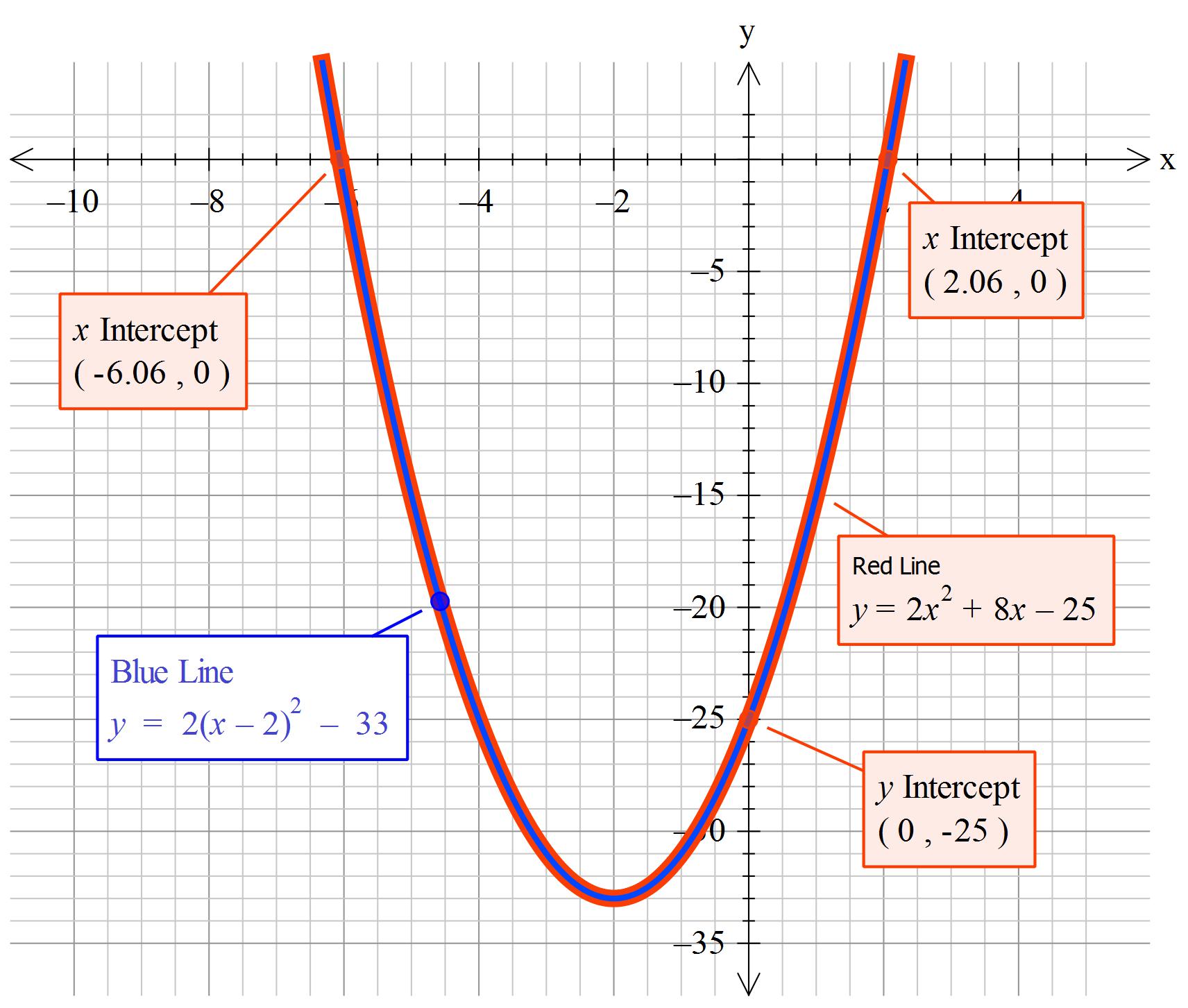
Given:#" "2x^2+8x-25=0# ....................Equation(1)
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(blue)("Completing the square")#
write as #y=2(x^2+4x)-25=0#
Introduce the correction k to compensate for the changes we are going to make. They introduce an error.
#2(x^2+4x)-25+k=0 larr" at this stage "k=0#
Take the power of 2 outside the brackets
#2(x+4x)^2-25+k=0 #
Remove the #x# from #4x#
#2(x+4)^2-25+k=0#
Halve the 4
#2(x+2)^2-25+k=0#............................. Equation(2)
From the part: #color(red)(2)(xcolor(blue)(+2))^2# you get the constant #color(red)(2)color(blue)(xx2)^2=8# which is the error.
so #8+k=0=> k=-8# Substituting into equation(2) gives
#2(x+2)^2-25-8=0............................. Equation(2_a)#
#2(x+2)^2-33=0#
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(blue)("Determine "x_("intercepts"))#
Write as#(x+2)^2=33/2#
Square root both sides
#x+2=sqrt(33/2)#
#=>x=-2+-sqrt(33/2)#
#=> x~~-6.06 " and " 2.06# to 2 decimal places