Question

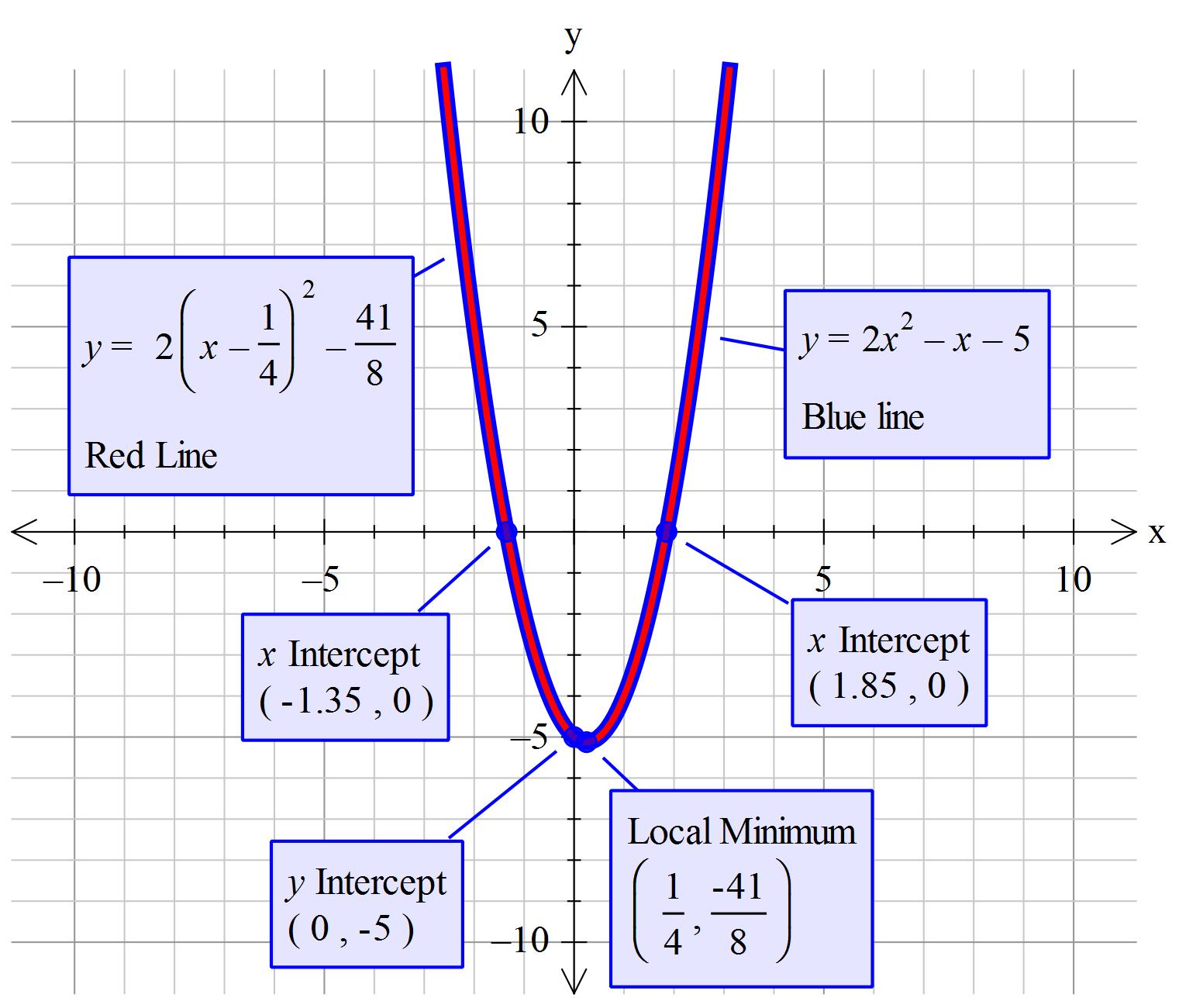
How do you solve using the completing the square method `2x^2 - x - 5 = 0`?

Answer 1

`" "2(x-1/4)^2-41/8 => "vertex" -> (x,y) -> (1/4,-41/8)`

x-axis and y-axis Intercepts can be found in the normal way

Explanation:

For a more in depth approach have a look at my solution to
http://socratic.org/s/asD9k2Ch. Diferent values but the method is sound.

Write as:`" "2(x^2-color(red)(1/2)x)-5=0`

For the `color(red)(-1/2)" in "-1/2x` apply: `(-1/2)xx(color(red)(-1/2)) = + 1/4`

So the left hand side becomes:

`" "2(x^2-1/4color(green)(x))-5`

Remove the `color(green)(x)`

`" "2(x^(color(magenta)(2))-1/4)-5`

Move the index (power) `color(magenta)(2)` to outside the brackets

`" "2(xcolor(red)(-1/4))^(color(magenta)(2)) -5`

Square the constant `color(red)((-1/4)^2=+1/16` and subtract twice its value `color(red)(2xx(=1/4)^2=+1/8)`

`" "2(x-1/4)^2-5-1/8`

`" "2(x-1/4)^2-41/8`

'~~~~~~~~~~~~~~~~~~~~~~~~~~~
`x_("vertex") = (-1)xx(-1/4)= +1/4`

`y_("vertex")= -41/8 =-5 1/8`