Question

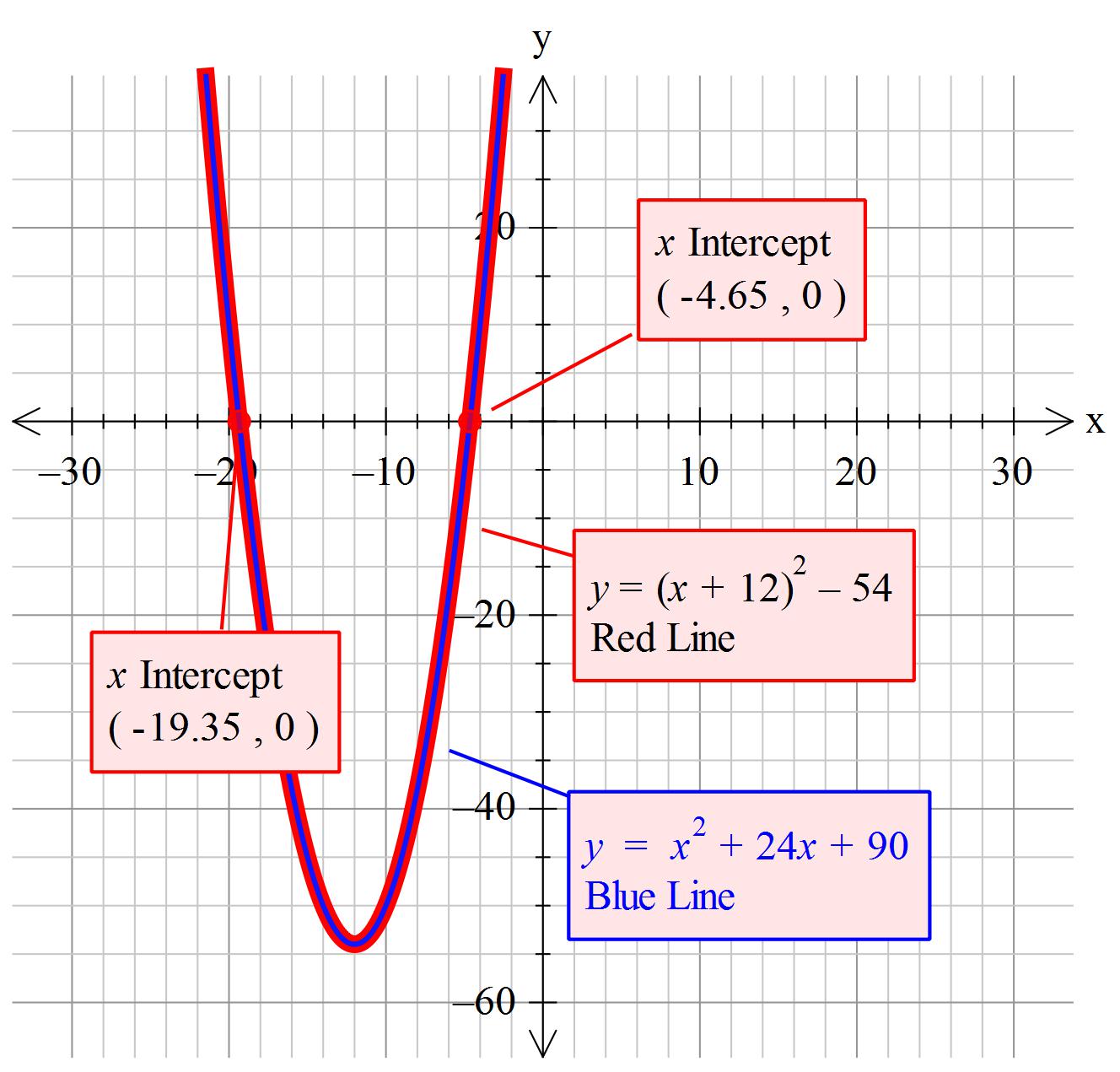
How do you solve using the completing the square method `x^2+24x+90=0`?

Answer 1

`(x+12)^2 -54=0`

Explanation:

The expression `(x+a)^2` expands as `x^2 + 2ax + a^2`
so to complete the square we use half the coefficient of the middle term to be `a`.

We then subtract the equivalent of `a^2` (in this case `12^2`) and add the final term (`90`).

`(x+12)^2 -144+90`
`=(x+12)^2 -54`

Answer 2

`=>x=-12+-3sqrt(6)" "` as exact values

`=> x~~-4.65" and "-19.35" "` to 2 decimal places

Explanation:

Standard for `" "y=ax^2+bx+c"`

Write as`" "y=a(x+b/(2a))^2 + c + (-b^2/(4a))`

The purpose of the `b^2/(4a)` is to mathematically remove an error that have been introduced by building `a(x+b/(2a))^2`

If you square `b/(2a)` then multiply it out by the variable `'a'` in front of the bracket you have introduced a value that was not in the original equation. So you remove it by subtraction.
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Given:`" "x^2+24x+90=0" "` Note that `a=1`

Write as:`" "y=(x+12)^2+90+k`

But `k=-(12)^2/4 = -144`

`color(brown)(" "=>y=(x+12)^2+90+k)color(blue)(" "->" "y=(x+12)^2-54)`
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

`x^2+24x+90=y=0=(x+12)^2-54`

So `(x+12)^2=+54`

`=>sqrt((x+12)^2)=sqrt(54)`

`=>x+12=+-sqrt(6xx3^2)`

`=>x=-12+-3sqrt(6)`

`=> x~~-4.65" and "-19.35` to 2 decimal places