How do you solve #x^2 + 10x + 13 = 0# by completing the square?
2 Answers
Explanation:
Given:
This process introduces an error that has to be compensated for. To do this I introduce a corrective as yet unknown value represented by
Compare to
This then written as a first step as:
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Move the square from
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Remove the
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Halve the 10
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
NOW WE DETERMINE THE VALUE OF
Just for demonstration lets multiply out the brackets and then compare what we have to the original equation.
For the new equation to work we must have
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Set
Add 12 to both sides
Square root both sides
Subtract 5 from both sides
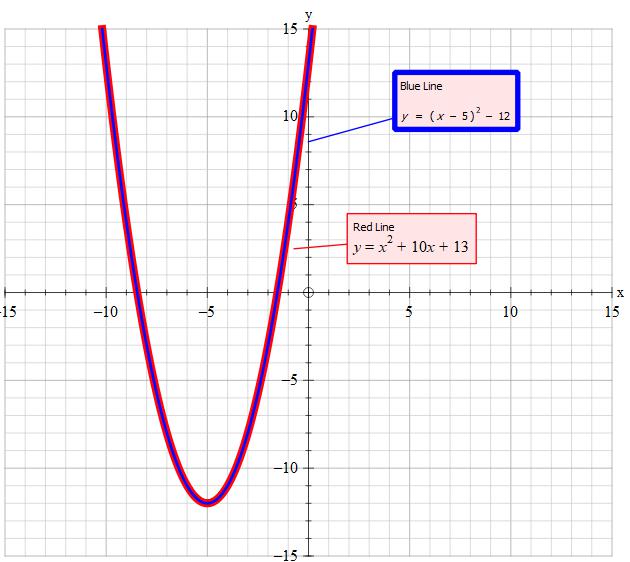
Explanation:
Start with
Subtract 13 from both sides:
Take 10, divide by 2, to get 5. Square 5 to get 25. Add 25 to both sides:
The left side is now a perfect square:
Now solve by taking the square root of both sides:
Subtract 5 from both sides:
Simplify the radical if you'd like:



