Given:#" "color(brown)(x^2+18=-81)#
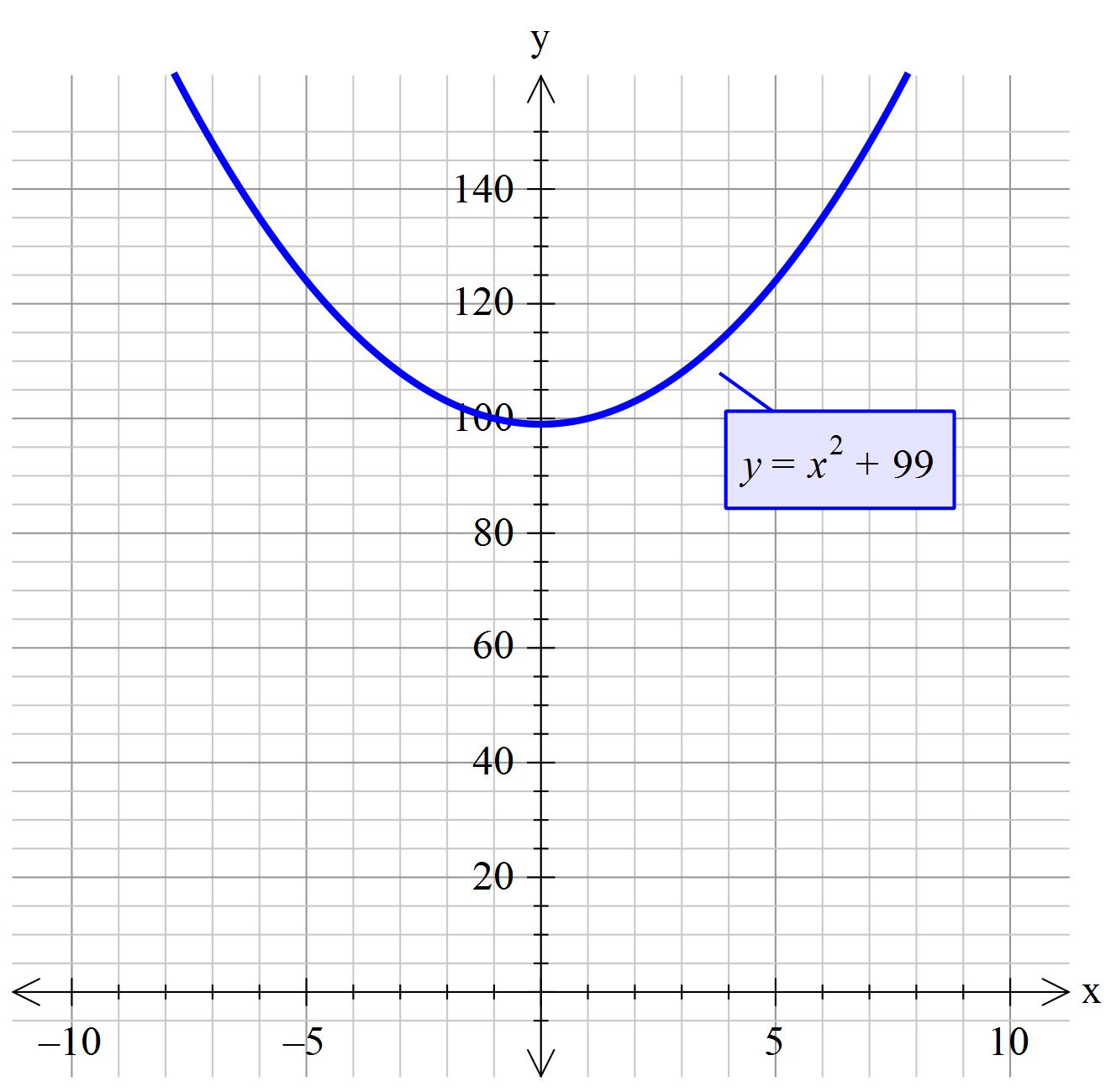
If so chosen you could write this as #y=x^2+99#
#color(blue)("Solving for "x" where the given equation is true")#
Subtract #color(blue)(18)# from both sides
#" "color(brown)(x^2+18color(blue)(-18)=-81color(blue)(-18))#
#" "x^2+0=-99#
know: #color(green)(3xx33=99)" so "color(blue)(3xx3xx11=99)" so "color(red)(3^2xx11=99)#
But we have negative 99 so we have #(-1)xx3^2xx11#
Thus our equation becomes
#x^2=(-1)xx3^2xx11#
Take the square root of each side
#x=+-sqrt((-1)xx3^2xx11)#
#=> x=+-3xxsqrt(11)sqrt(-1)#
But #sqrt(-1)=i#
#color(blue)(=>x=+-3isqrt(11))#
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Notice that the graph does not cross the x-axis.
But by writing the equation as #x^2+18=-81#
#y=x^2+99#
So to solve for #x# we have to write
#y=0=x^2+99# but for #y=0# implies that the graph crosses the x-axis when in fact it does not. So to be able to solve for #y=# we introduce 'complex numbers'. Hence the #sqrt(-1)#