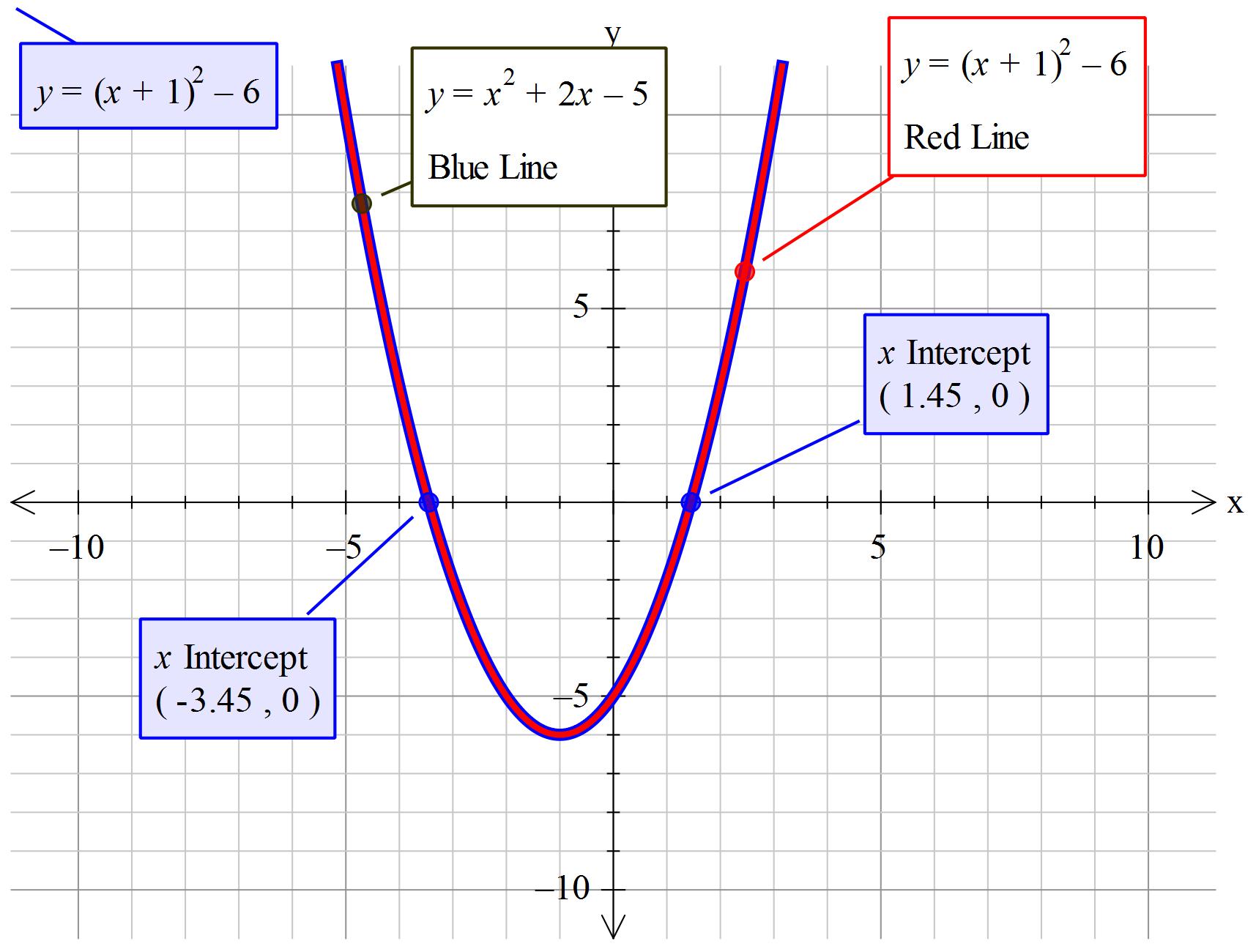
How do you solve #x^2+2x-5=0#?
3 Answers
Explanation:
Use the improved quadratic formula (Google, Yahoo Search)
There are 2 real roots:
Explanation:
#color(blue)(x^2+2x-5=0#
This is a Quadratic equation (in form
Use Quadratic equation
#color(brown)(x=(-b+-sqrt(b^2-4ac))/(2a)#
Where
Explanation:
Another approach would be to complete the square. It is another form of the standard
Given:
Note that standard form of
The error comes from
So
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Taking the square root of both sides
But for this question