How do you solve #x^2-3x = 28#?
3 Answers
Explanation:
Some times you can spot the factors other times not so easy. If you are ever really stuck and the method of solution is not fixed use the formula or complete the square.
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Given:
Subtract 28 from both sides
Notice that
So
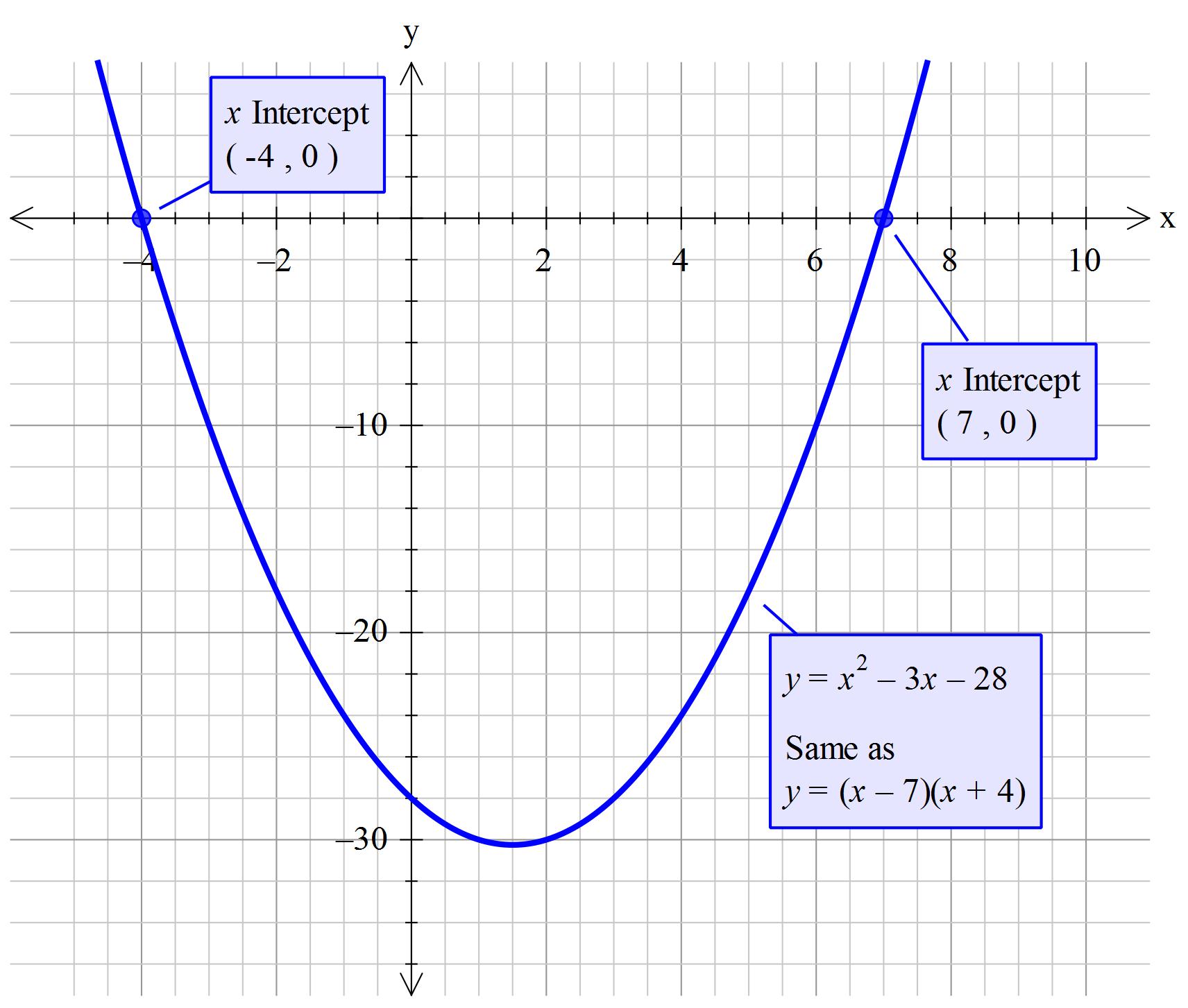
Explanation:
Write in the standard quadratic form
Factorise
For this to be true either
Hence the answer
Explanation:
Factorise:
or
Hence: