How do you solve #x^2 + 3x - 4 = 0# graphically and algebraically?

Question

16652 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-07-22T10:01:35

#x=1#
#x=-4#

Given -

#x^2+3x-4=0#

Algebraic Solution

#x^2-x+4x-4=0#
#x(x-1)+4(x-1)=0#
#(x-1)(x+4)=0#
#x=1#
#x=-4#

If you take the above equation as a function as

#y=x^2+3x-4#

One Solution is

#(1, 0)#

Another solution is

#(-4,0)#

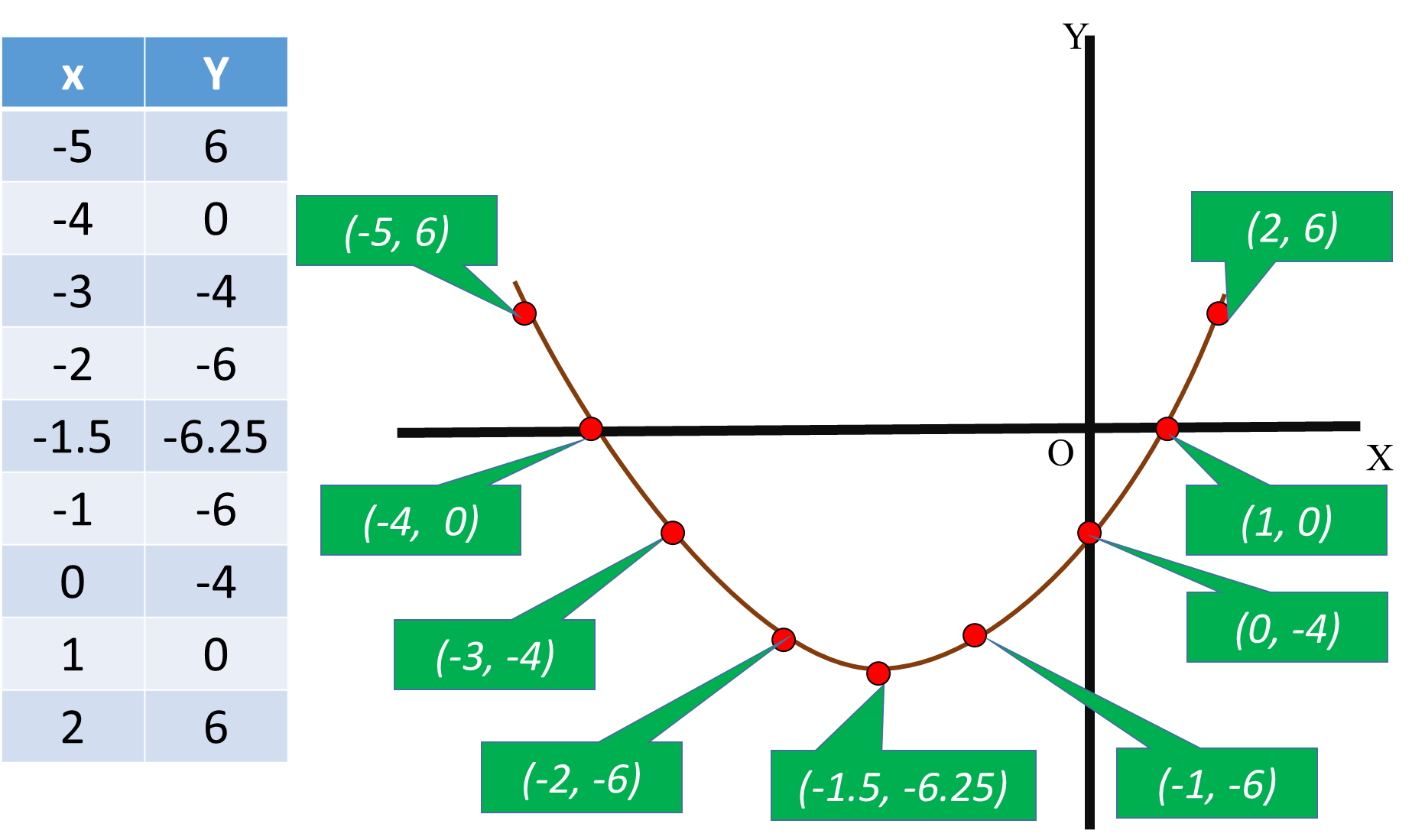
To have a graphic solution, You have identify a range of

values for #x# That includes vertex and the above said two points.

Its vertex is given by -

#x=(-b)/(2xxa)=(-3)/(2 xx1)=-3/2#

Now take four values above and below #-3/2#

Find the corresponding #y# values for #x#

Plot all the values. Those co-ordinates where the curve cuts the x-axis is the graphic solution to the problem.

Look at the image for solution