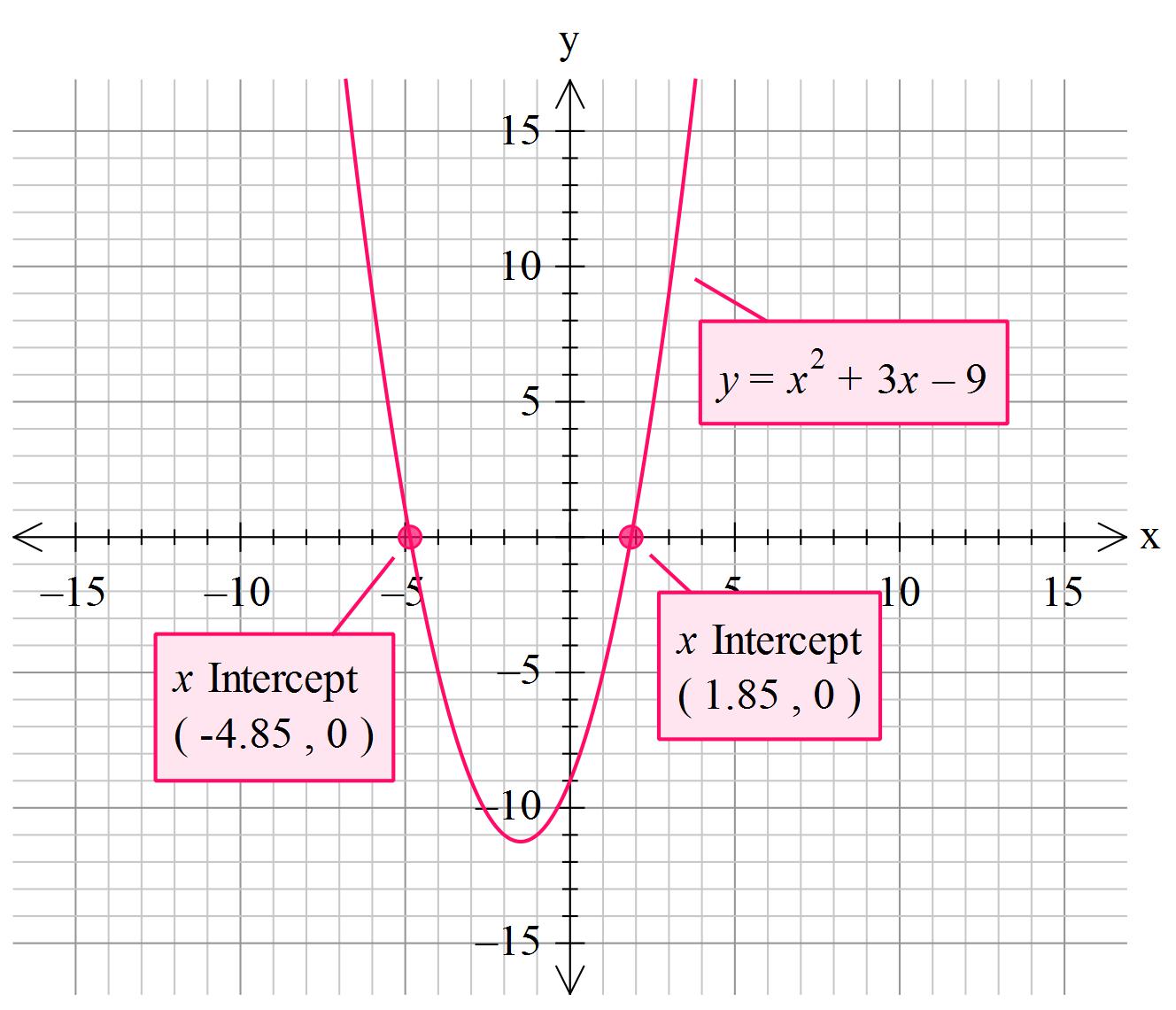
Not that standard form is #y=ax^2+bx+c#
and that vertex form is #y=color(red)(a)(x+color(red)(b/(2a)))^2+c +k#
where #k# is a correction constant in your case #a=1#
'~~~~~~~~~~~~~~~~~~~~~~~~~~~
Given:#" "y=x^2+3x-9=0#
write as: #0=(x^2+3x)-9#
Add the correction constant #k#
#0=(x^2+3x)-9+k#
Remove the #x# from #3x#
#0=(x^2+3)-9+k#
Halve the 3
#0=(x^2+3/2)-9+k#
Move the power from #x^2# to outside the bracket
#0=(x+3/2)^2-9+k" "color(red)(larr "the error comes from "a(3/(2a))^2)#
but #k+(3/2)^2=0 => k=-9/4# giving
#color(blue)("Vertex form "->0=(x+3/2)^2- 45/4#
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Take the #-45/4# to the other side of the equals and change its sign.
#(x+3/2)^2=+45/4#
Square root both sides
#x+3/2=sqrt(45/4)#
Move the #3/2# to the other side of =
#x=-3/2+-sqrt(5xx9)/sqrt(4)#
#color(blue)(x=-3/2+-(3sqrt(5))/2)#
#color(blue)(x~~1.854" "and" " -4.854 ) #