Question

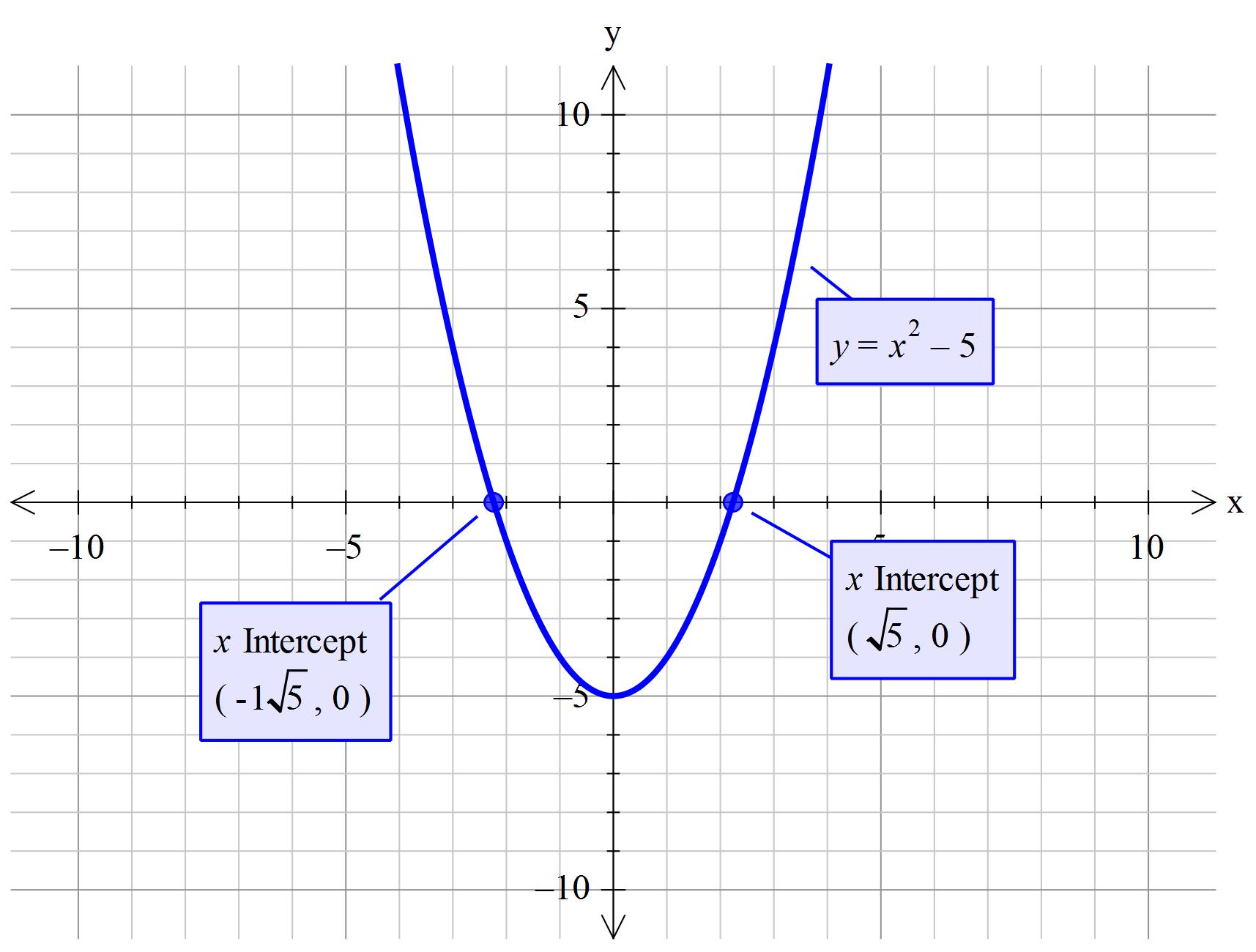
How do you solve `x^2-5=0` graphically and algebraically?

Answer 1

`x=+-sqrt(5)` exactly, or approximately `+-2.236` to 3 decimal places

Explanation:

Given:`" " x^2=5=0`

To solve mathematically we need to have just 1 `x` and for it to be on one side of the equals sign and everything else on the other side.

To get the x term on its own.

Add `color(blue)(5)` to both sides of the equation

`" "color(brown)(x^2-5color(blue)(+5)=0color(blue)(+5)`

`x^2+0=5`

`x^2=5`

But `x^2` is the same as `x xx x` and we need to have just 1 not 2 of them.

Take the square root of both sides

`sqrt(x^2)=sqrt(5)`

So `x=sqrt(5)" "` which is 2.236 to 3 decimal places

But both `(-2.236 )xx(-2.236 ) = 5" "`

and`" "(+2.236 )xx(+2.236 )=5`

So `x=+-sqrt(5)` exactly or approximately `+-2.236` to 3 decimal places

'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~