How do you solve #x^2 - 5x+ 6 = 0#?
1 Answer
Jan 11, 2018
Explanation:
Given:
Step.1
Consider
Split the middle term of the Quadratic Expression:
We can rewrite this in factor form:
Hence,
the factors are:
This would mean
either
Now we can write our solutions as
We can also graph our quadratic to verify our solutions
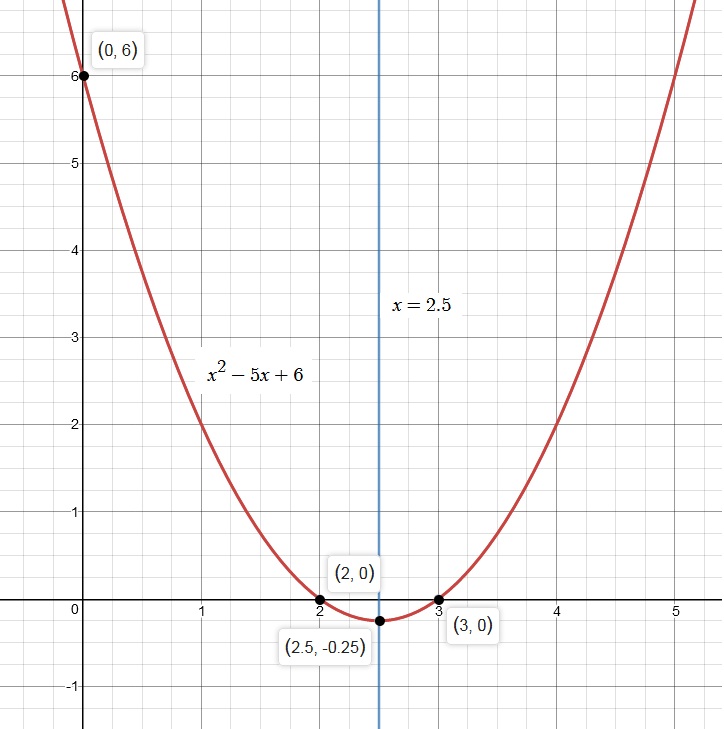
We analyze the graph and note the following:
x-intercepts are:
Hence, our solutions are verified.
Some additional pieces of useful information for you:
Vertex is at
And,
Axis of Symmetry is at

