How do you solve #x - 2y = -6# and #-x + y = 2#?

Question

10579 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-06-09T18:20:49

I got:
#x=2#
#y=4#

Have a look:

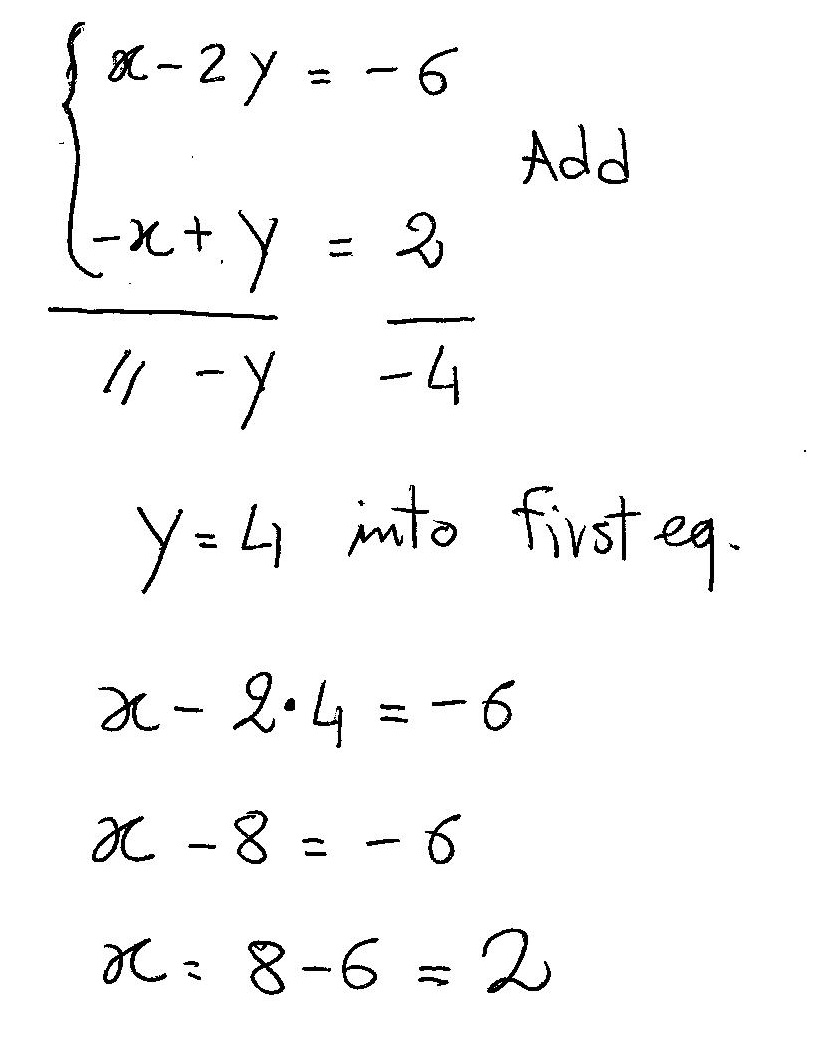
enter image source here

Answer 2 · 2017-06-09T19:25:29

#x=2 and y=4#

Make #x# the subject of both equations:

#x= 2y-6" and "x= y-2#

The value of #x# is the same, so if:

#" "x = x# then:
#2y-6 = y-2" "larr# solve for #y#

#2y-y= -2+6#

#y =4#

#x = 2(4) -6#

#x=8-6#

#x=2#

Answer 3 · 2017-06-09T19:35:36

#x=2#
#y=4#

We could also solve this problem using substitution.

Solve the 1st equation for #x#:

#x-2y=-6#

#x=2y-6#

Substitute the above into the 2nd equation and solve for #y#:

#-x+y=2#

#-(2y-6)+y=2#

#-2y+6+y=2#

#-y=-4#

#y=4#

Substitute #y# into the 1st equation and solve for #x#:

#x-2y=-6#

#x-2(4)=-6#

#x=2#