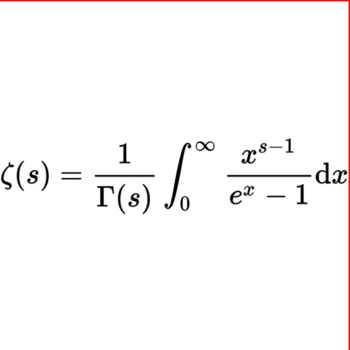How do you subtract #\frac { 6} { 13a } - \frac { 4} { 13a ^ { 2} }#?
3 Answers
Explanation:
In order to subtract two fractions, we need to find the lowest common multiple of their denominators.
For
So we need to multiply
We can now subtract the two fractions.
See the entire solution process below:
Explanation:
To be able to add or subtract fractions they must be over common denominators. To put the fraction on the left in the expression over a common denominator we need to multiply it by the appropriate form of
We can now subtract the numerators over the common denominator:
Explanation:
Multiply the numerator and the denominator of the first fraction by
You might ask yourself how we could multiply the numerator and the denominator of a fraction by a number, doesn't that changes the answer?
The answer is no, it does not change the answer thus