How do you test #f(x)=8 x^4−9 x^3 +9# for concavity and inflection points?
1 Answer
Explanation:
To test for the concavity and inflection points you need to equate the second order derivative with zero.
Keeping in mind:
-
#d/dxx^n=nx^(n-1)# -
#d/dxc=0#
We proceed:
Now,
graph{x(16x -9) [-5, 5, -5, 5]}
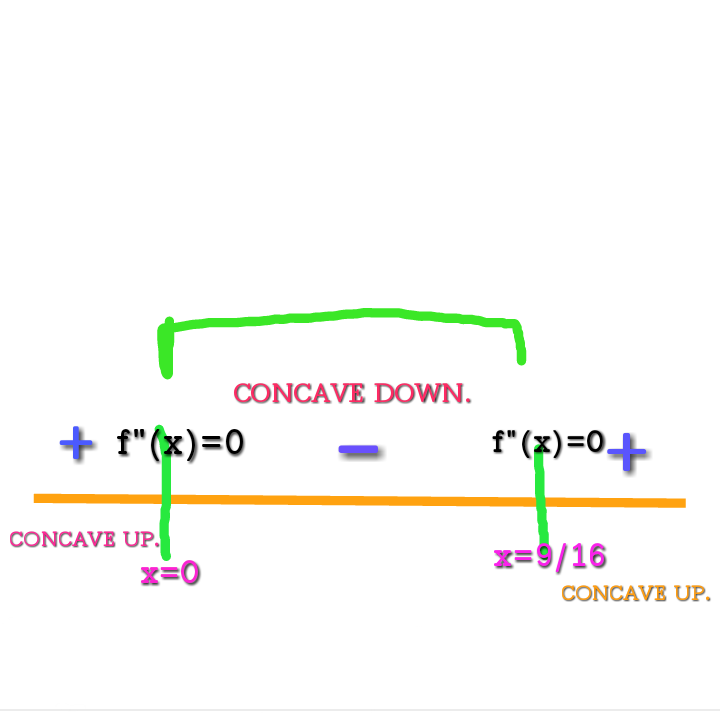
Sign Chart: See image.
Now, to determine the opening of the concavity.
- Put any value less than
#0# in#f''(x)# .
- Put any value between
#0# to#9/(16)# .
- Put any value greater than
#9/(16)# .
Negative sign indicates that the curve will open downwards. And positive sign indicates it'll open up.
Thus,
And,
Hope this helps. :)

