Question

How do you use a half-angle formula to find the exact value of `cos22.5`?

Answer 1

`color(maroon)(cos 22.5^@ = + sqrt((sqrt2 -1)/(2 sqrt2)) ~~ + 0.3827`

Explanation:

`cos (theta/2) = +- sqrt((1-cos theta) / 2)`

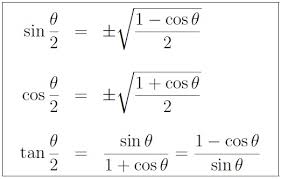
Let `hat (theta/2) = 22.5^@`

`hat theta = 2 * 22.5 = 45 ^@`

cos (theta/2) = cos 22.5^@ = + sqrt((1 - cos 45) / 2)#

We know `cos 45 = 1 / sqrt2`

`:. color(maroon)(cos 22.5^@ = + sqrt((1 - 1/sqrt2)/2) = + sqrt((sqrt2 -1)/(2 sqrt2)) ~~ + 0.3827`

Answer 2

`cos22.5^@=1/2(sqrt(2+sqrt2))`

Explanation:

`"using the "color(blue)"half-angle formula for cos"`

`•color(white)(x)cos(x/2)=+-sqrt((1+cosx)/2)`

`cos22.5^@=+sqrt((1+cos45^@)/2)`

`color(white)(xxxxxx)=sqrt((1+sqrt2/2)/2)`

`color(white)(xxxxxx)=sqrt((2+sqrt2)/4)`

`color(white)(xxxxxx)=1/2(sqrt(2+sqrt2))`