Question

How do you use Newton's method to find the two real solutions of the equation `x^4-x^3-3x^2-x+1=0`?

Answer 1

The roots of the equation `x^4-x^3-3x^2-x+1 =0` are `0.4221` and `2.3692` to 4dp.

Explanation:

First let us look at the graphs (not strictly needed but it gives s insight into the problem):

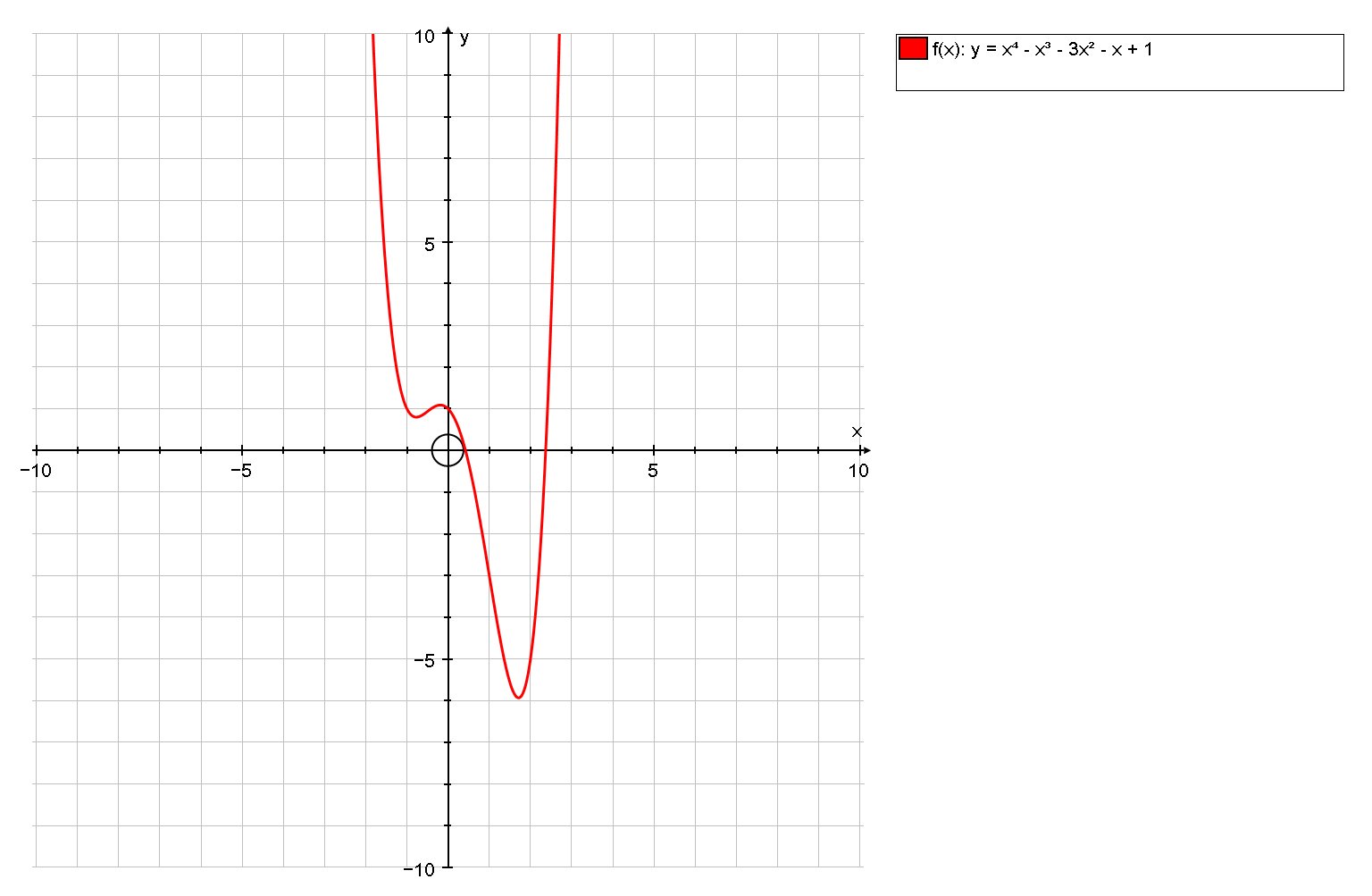
We can see there are two solutions. There is one solution in the interval `0 < x < -1` and a second solution in the interval `2 < x < 3`. We can find the solution to `f(x)-0` numerically, using Newton-Rhapson method.

Let

`\ \ f(x) = x^4-x^3-3x^2-x+1 =>`
`f'(x) = 4x^3-3x^2-6x-1`

and we will need to apply the Newton-Rhapson method twice to find both roots. We use the following iterative sequence

`{ (x_0=alpha), ( x_(n+1)=x_n - f(x_n)/(f'(x_n)) ) :}`

To find the first root (arbitrarily) choose `alpha=1`

Then using excel (working to 6dp) we can tabulate the iterations as follows:

To find the second root (arbitrarily) choose `alpha=3`

We would need to vary `alpha` if the NR Method diverged or provided the incorrect root.

And so we conclude that the roots of the equation

`x^4-x^3-3x^2-x+1 =0`

are `0.4221` and `2.3692` to 4dp.