Question

How do you use symmetry-adapted linear combinations to explain water's molecular bonding?

Answer 1

An interesting use of the wave function (found in the context of the Schrodinger equation) is for symmetry-adapted linear combinations. Just a heads-up that this is a difficult topic, so don't feel bad if it seems confusing.

---

WAVE FUNCTIONS CAN HELP YOU PREDICT ORBITAL INTERACTIONS

The idea is, if two orbitals transform under different symmetries, they cannot merge to form molecular orbitals, regardless of whether they have similar energies or not.

Let's say we looked at the water molecule. Drawing it out on xyz coordinate axes, we get:

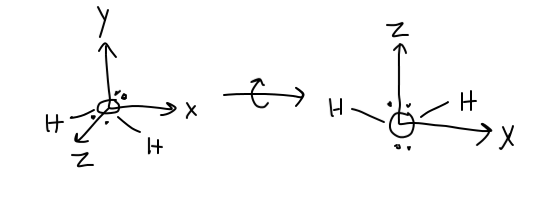
Now, there's something called a point group that every molecule belongs to, which can describe the ways the atomic orbitals of the central atom of choice and the group orbitals of the other atoms respond to symmetry operations.

When we draw symmetry elements (like axes and planes) onto water, we get that:

• It can do nothing, and achieve itself, indicating the identity operation `hatE`. Simple enough.
• It can rotate around the z-axis `180^@` before it becomes indistinguishable from the previous orientation. We call that the proper rotation operation `hatC_2` around the `C_2` axis because it takes two `180^@` rotations to go around `360^@` and achieve the identical molecule back.
• It can be reflected over the xz-plane to give itself, which follows the vertical reflection plane operation `hatsigma_v(xz)`.
• It can be reflected over the yz-plane to give itself, which follows the vertical reflection plane operation `hatsigma_v(yz)`.

It has no other symmetry elements. Since it has no `C_2'` axis perpendicular to the `C_2`, it only has one `C_2` axis (rotating about the y-axis takes `360^@` to get back to a form indistinguishable from the original, which is really just `hatE` again).

Overall that means it is a `C_(2v)` point group. What does that mean? Well, each point group corresponds to what's called a character table:

http://www.webqc.org/symmetrypointgroup-c2v.html

The key aspects we are going to take from this are:

• `A_1, A_2, B_1, B_2` are the "irreducible representations" for each symmetry operation, which describe how the wave function changes upon the symmetry operation (rotate, flip, etc).
• `1` means the wave function being operated upon did not change sign.
• `-1` means it did.

SYMMETRY OF OXYGEN'S VALENCE ORBITALS

If we examine oxygen's valence orbitals, we get that it has a `2s`, `2p_x`, `2p_y`, and `2p_z`. Now, imagine operating on them in space with the `hatE`, `hatC_2`, `hatsigma_v(xz)`, and `hatsigma_v(yz)` operations.

The wave function `psi` may or may not change sign, depending on its equation. Skipping past `hatE` (because it literally does nothing), we get:

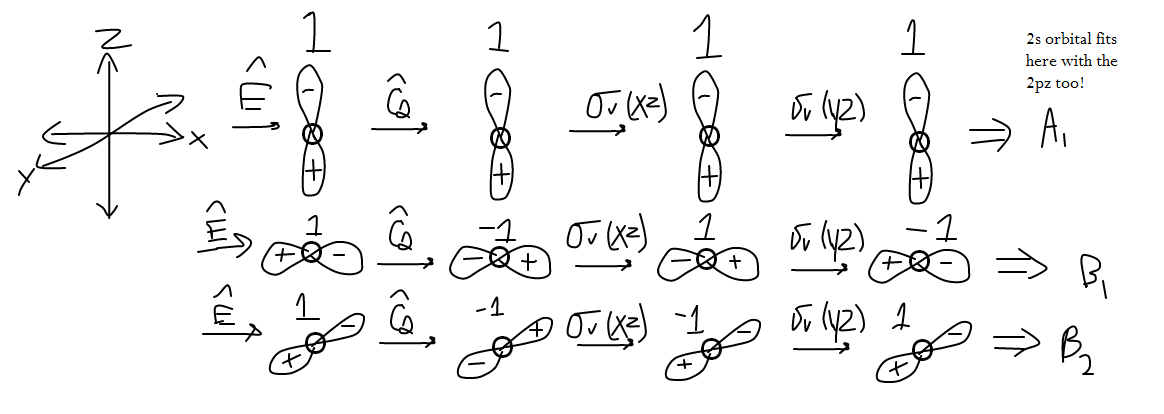
These operations all return `1` if the orbital stayed the same, `-1` if the orbital lobe signs switched places, or `0` if two different coordinates get swapped (e.g. `x harr y`).

If you look carefully, you may notice that the resultant orbital transformations correspond to the numbers in the character table above, which is how I decided what each orbital corresponds to.

`A_1`, `A_2`, `B_1`, and `B_2` are what are called irreducible representations (IRREPs). They are the most reduced representations that describe the way an orbital changes due to symmetry operations. For these IRREPs, the lowest terms are `pm1`.

`A_1` reads `1,1,1,1` from left to right, `B_1` reads `1,-1,1,-1` from left to right, and so on.

I glossed over the `2s` orbital because it is a sphere, so it automatically belongs to `A_1` for its perfect symmetry and singular lobe sign (its wave function cannot change sign upon any operations).

SYMMETRY OF HYDROGENS' GROUP ORBITALS

Now we move on to hydrogen. Here's where things get really tricky, so ask questions if you need to.

Let us choose the left hydrogen as our basis of transformation. Since there are two hydrogens and not one, we have to start with a reducible representation, and reduce it to the irreducible representation. Kind of a hassle, but nevertheless, we have to do it.

The operations give us:

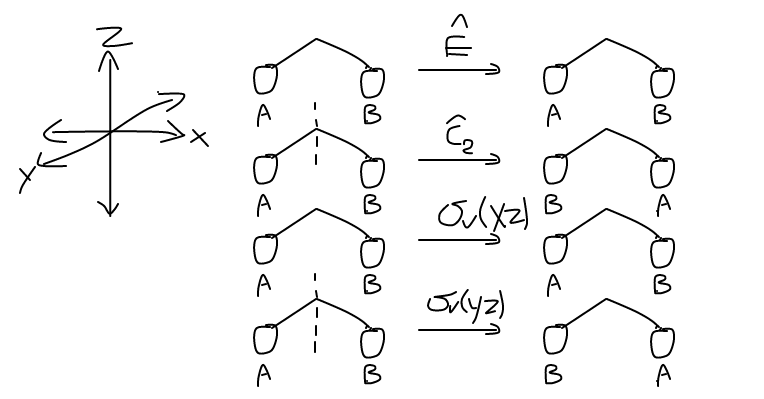
• The `hatE` leaves the `1s` orbitals alone, and there are two in the basis, so this returns `1` per orbital, giving `\mathbf(2)`. `H_a -> H_a`, and `H_b -> H_b`.
• The `hatC_2` operation switches the coordinates of the two `1s` orbitals, returning `\mathbf(0)`. `H_a -> H_b`, and `H_b -> H_a`.
• The `hatsigma_v(xz)` operation reflects the two `1s` orbitals, giving back the same orbitals with the same lobe sign (whichever signs they happen to be), and there are two orbitals, so this returns `\mathbf(2)`. `H_a -> H_a`, and `H_b -> H_b`.
• The `hatsigma_v(yz)` operation reflects the two `1s` orbitals in such a way that they swap coordinates with each other, so they end up returning `\mathbf(0)`. `H_a -> H_b`, and `H_b -> H_a`.

Therefore, our reducible representation is:

`color(green)(Gamma = "2 0 2 0")`

Reducing it takes some tricks with character tables that I don't want to go too much into, but the calculations turn out to be:

`color(blue)(Gamma_(A_1)) = 1/(1+1+1+1)*[1*2*1 + 1*0*1 + 1*2*1 + 1*0*1] = color(blue)(1)`

`color(blue)(Gamma_(A_2)) = 1/(1+1+1+1)*[1*2*1 + 1*0*1 + 1*2*-1 + 1*0*-1] = color(blue)(0)`

`color(blue)(Gamma_(B_1)) = 1/(1+1+1+1)*[1*2*1 + 1*0*-1 + 1*2*1 + 1*0*-1] = color(blue)(1)`

`color(blue)(Gamma_(B_2)) = 1/(1+1+1+1)*[1*2*1 + 1*0*-1 + 1*2*-1 + 1*0*1] = color(blue)(0)`

We can write that as the IRREP `\mathbf(A_1 + B_1)`.

For these `1s` orbitals, it is not too difficult to draw the group orbitals; either both orbitals are in phase, or they are out of phase with each other.

The in-phase ones are `A_1` because all transformations return `1`. The out-of-phase ones are `B_1` because the rotation around the z-axis and reflection over the yz-plane switch the sign of the orbitals (wave function).

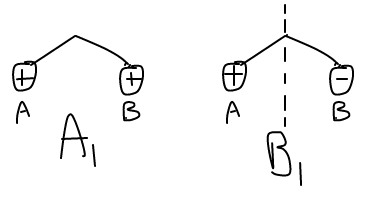
INTERACTION OF HYDROGEN'S GROUP ORBITALS WITH OXYGEN'S ATOMIC ORBITALS

Ultimately, we have determined the symmetries for each orbital:

• Oxygen's atomic orbitals correspond as `[2s, 2p_z] harr A_1`, `2p_x harr B_1`, and `2p_y harr B_2`.
• Hydrogen's group orbitals correspond as `2s harr A_1, B_1`

Since only orbitals of the same symmetry can overlap, hydrogen can only overlap its `sigma"/"sigma^"*"` group orbitals with oxygen's `2s`, `2p_x`, and `2p_z`.

It just so happens that the `2p_y` (the one going out of the plane) is the wrong symmetry and therefore cannot overlap with hydrogen's `2s` orbitals.

So, we should expect it to yield a nonbonding molecular orbital (`1b_1`).

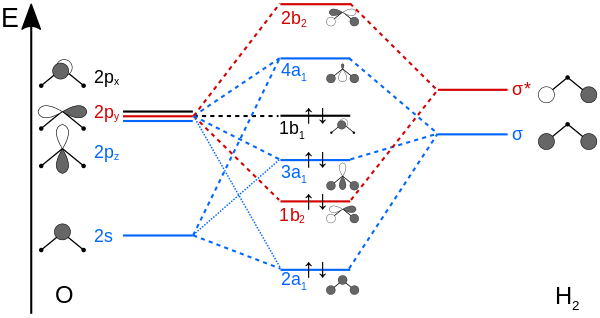https://upload.wikimedia.org/

(in the diagram, the coordinates axes are different; switch `x` with `y` and you'll have it.)

When the `2p_z`, `2p_y`, and `2p_x` mix with the `2s`, the `2s` and `2p_y` combination yield one nonbonding `1b_1` orbital, while the resultant `sp^3` hybrid orbitals that do form successful molecular orbitals allow for two `sigma` bonds.

The nonbonding `1b_1` orbital (from our `2p_y (O)`) holds one lone pair of electrons, and the other lone pair is held by the `3a_1` orbital (from `2s (H) + 2p_z (O)`).