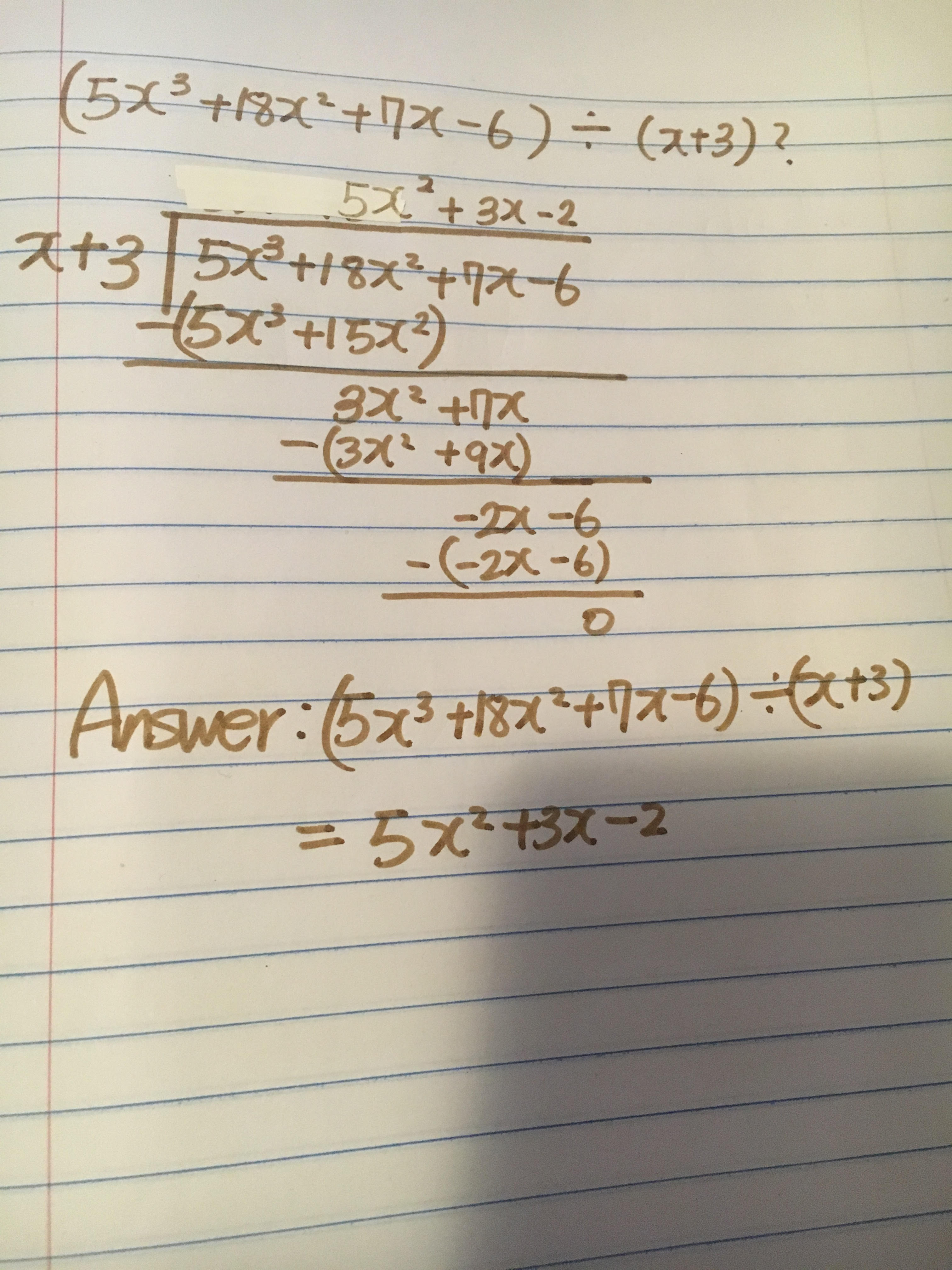To divide #f(2)# for #5x^3+18x^2+7x-6# by #x+3#
One Write the coefficients of #x# in the dividend inside an upside-down division symbol.
#color(white)(1)|color(white)(X)5" "color(white)(X)18color(white)(XX)+7" "" "-6#
#color(white)(1)|" "color(white)(X)#
#" "stackrel("—————————————)#
Two Put #-3# in the divisor at the left as #x+3=0# gives #x=-3#
#-3|color(white)(X)5" "color(white)(X)18color(white)(XX)7" "" "-6#
#color(white)(xx)|" "color(white)(X)#
#" "stackrel("—————————————)#
Three Drop the first coefficient of the dividend below the division symbol.
#-3|color(white)(X)5" "color(white)(X)18color(white)(XX)7" "" "-6#
#color(white)(xx)|" "color(white)(X)#
#" "stackrel("—————————————)#
#" "color(white)(1)|color(white)(X)color(red)#
Four Multiply the result by the constant, and put the product in the next column.
#-3|color(white)(X)5" "color(white)(X)18color(white)(XX)7" "" "-6#
#color(white)(xx)|" "color(white)(X)#
#" "stackrel("—————————————)#
#" "color(white)(1)|color(white)(X)color(blue)5#
Five Add down the column.
#-3|color(white)(X)5" "color(white)(X)18color(white)(XX)7" "" "-6#
#" "color(white)(1)|" "color(white)(X)-15#
#color(white)(1)stackrel("—————————————)#
#color(white)(xx)|color(white)(X)color(blue)5color(white)(XXX)color(red)3#
Six Repeat Steps Four and Five until you can go no farther.
#-3|color(white)(X)5" "color(white)(X)18color(white)(XX)7" "" "-6#
#" "color(white)(1)|" "color(white)(X)-15color(white)(X)-9color(white)(XXX)6#
#color(white)(1)stackrel("—————————————)#
#color(white)(xx)|color(white)(X)color(blue)5color(white)(XXX)color(red)3color(white)(X)color(red)-2color(white)(XXX)color(red)0#
Hence remainder is #0# and quotient is #5x^2+3x-2#