Question

How do you use the binomial `(2t-s)^5` using Pascal's triangle?

Answer 1

`(2t-s)^5=32 t^5-80st^4 +80s^2t^3- 40t^2s^3+ 10ts^4 -s^5`

Explanation:

Pascal's triangle:

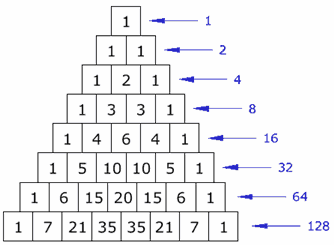
The sixth row, which corresponds to a binomial raised to the fifth power, shows us the coefficient of each term of that expansion. So the first term has coefficient `1`, the second term `6`, etc.

We also know that, for a binomial raised to `n`, one nomial in each term will have decreasing exponents from `n` to `0` and the other nomial will have increasing exponents from `0` to `n`.

`therefore(2t-s)^5=1(2t)^5(-s)^0+6(2t)^4(-s)^1+10(2t)^3(-s)^2+10(2t)^2(-s)^3+6(2t)^1(-s)^4+1(2t)^0(-s)^5`
`=32 t^5-80st^4 +80s^2t^3- 40t^2s^3+ 10ts^4 -s^5`