How do you use the law of cosines to find the area of a triangle?
1 Answer
The area of a triangle is defined as: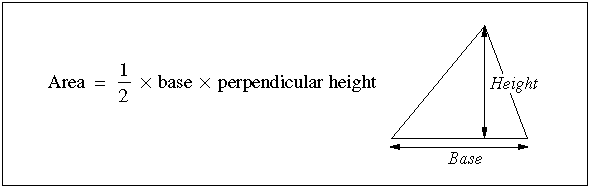
The law of cosines is useful when you know two sides and the angle between them, or when you know all three sides. Lets take a look at a generic triangle, ABC;
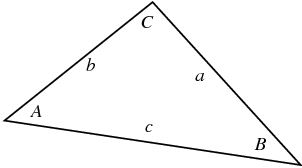
In the case that you know two sides and an angle, say sides a and b and angle C, you would simply use the area formula;
and there is no need to use the law of cosines.
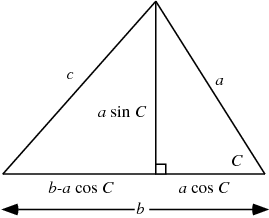
Therefore, lets look at the case where we know the three sides of a triangle, a, b, and c. In this case we cannot find the height by using sin(C). We can, however, use Pythagoras' theorem.
In the second image above, we would use Pythagoras' theorem to find the length of
Now we use the law of cosines to find
so we now have;
or;
It's not pretty, but we can plug this equation into our area equation to get;
where side

