How do you use the matrix method to solve the system of equations #5x+3y = 3# and #2x-6y=30#?
2 Answers
Apr 30, 2017
I got:
Explanation:
We can try using Cramer's Method:
1) evaluate the determinant of the matrix
2) evaluate the determinant of the matrix
3) find
4) evaluate the determinant of the matrix
5) find
Apr 30, 2017
#x=3#
#y=-4#
Explanation:
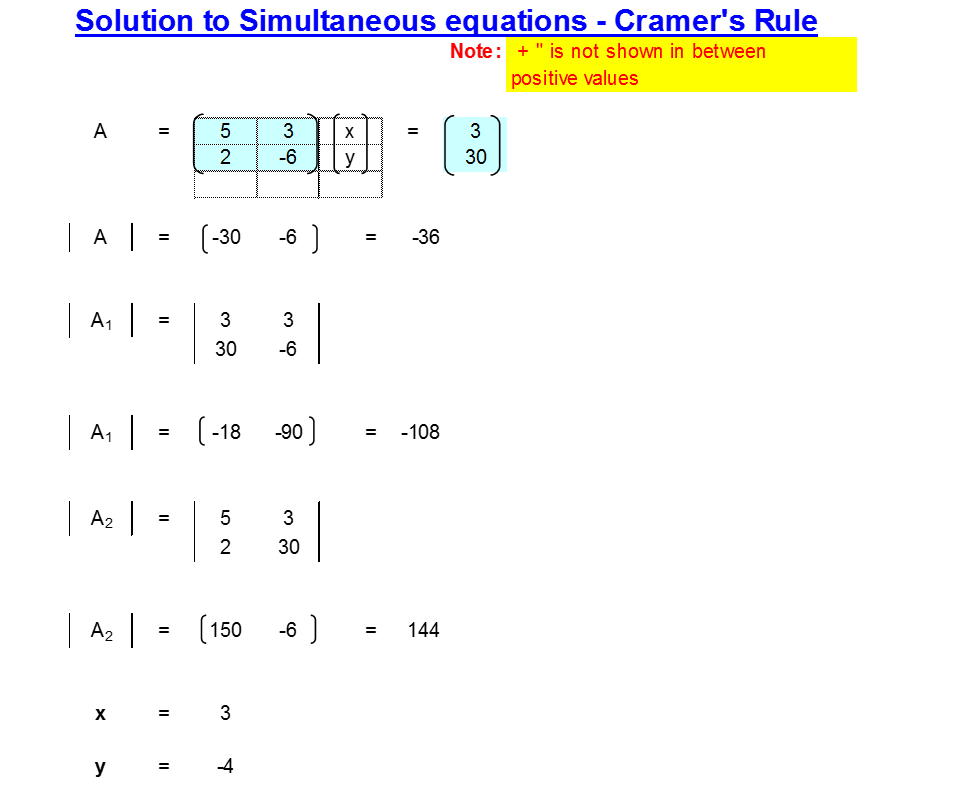
#x=A_1/A=(-108)/(-36)=3#
#y=A_2/A=(144)/(-36)=-4#


