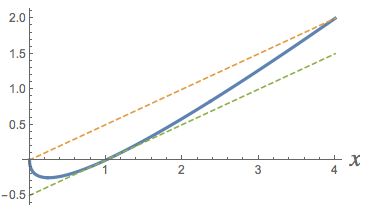
I assume in your question that you desire to find a value #c# between 0 and 4 so that #f'(c)=\frac{f(4)-f(0)}{4-0}=\frac{2-0}{4-0}=\frac{1}{2}#. Since #f'(c)=1-\frac{1}{2}c^{-1/2}#, that means you want to solve the equation #1-\frac{1}{2}c^{-1/2}=\frac{1}{2}# for #c#. This equation can be rearranged to say that #\frac{1}{2c^{1/2}}=\frac{1}{2}# so that #c^{1/2}=1#. This tells you that #c=1#.
A comment about what we are really doing here: we are not really "using" the Mean Value Theorem to solve anything. Rather, we are solving an algebra equation related to the instantaneous rate of change #f'(c)# and the average rate of change #\frac{f(4)-f(0)}{4-0}# to find the value of #c# that is guaranteed to exist by the Mean Value Theorem over the interval #[0,4]# (a value of #c# where the instantaneous rate of change equals the average rate of change). In effect, we are just illustrating the truth of the theorem, not using it.
Here's a picture of the situation in this problem. Note that the two dashed lines have equal slopes: